AT_pakencamp_2024_day1_l Taxi of Paken Kingdom

在「パ研王国」有 $N$ 个城市，编号为 $1, 2, \ldots, N$，以及 $M$ 条双向道路，编号为 $1, 2, \ldots, M$，每条道路连接着不同的两个城市。第 $i$ 条道路（$1 \leq i \leq M$）连接城市 $A_i$ 和城市 $B_i$，且不会有两条不同的道路连接同一对城市。从任意一个城市出发，都可以通过 $0$ 条或多条道路移动到任意其它城市，但不能不经过道路直接移动到其他城市。 现在是一年一度「パ研合宿」的季节，合宿将在城市 $1$ 举办，因此所有城市的参与者都需要前往城市 $1$。因为搬运行李很辛苦，参与者们会选择打出租车移动。 在「パ研王国」有 $N$ 家出租车公司，编号为 $1, 2, \ldots, N$，每家公司有如下规定： - 第 $i$ 家出租车公司的出租车只能在城市 $i$ 上车。 - 第 $i$ 家公司的出租车不论移动距离多少，费用都是 $C_i$。 - 第 $i$ 家公司的出租车最多只能经过 $R_i$ 条道路。 参与者可以多次换乘不同公司的出租车，但除了乘坐出租车以外，不能通过其他方式移动到其它城市。 请你计算，从每个城市出发，只使用出租车到达城市 $1$ 所需支付的最小总费用。可以保证在上述限制下，从所有城市出发都至少有一种方案只用出租车即可到达城市 $1$。

输入将通过标准输入按如下格式给出： > $N$ $M$ > $A_1$ $B_1$ > $A_2$ $B_2$ > $\vdots$ > $A_M$ $B_M$ > $C_1$ $C_2$ $\ldots$ $C_N$ > $R_1$ $R_2$ $\ldots$ $R_N$

请输出 $N$ 行，第 $i$ 行（$1 \leq i \leq N$）表示从城市 $i$ 出发，只使用出租车到达城市 $1$ 所需支付的最小总费用。

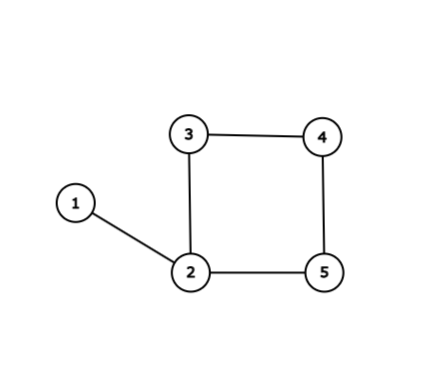
### 样例解释 1 「パ研王国」的结构如下：  例如，从城市 $5$ 到城市 $1$ 的一条可行路线如下： 1. 在城市 $5$ 乘坐第 $5$ 家出租车公司出租车，到达城市 $4$。 2. 在城市 $4$ 乘坐第 $4$ 家出租车公司出租车，到达城市 $1$。 此时总费用为 $100+200=300$。没有比 $300$ 更小的成本方案，因此应输出 $300$。 ### 数据范围 - $2 \leq N \leq 2 \times 10^5$ - $1 \leq M \leq 2 \times 10^5$ - $1 \leq A_i < B_i \leq N$ （$1 \leq i \leq M$） - $(A_i, B_i) \neq (A_j, B_j)$ （$1 \leq i < j \leq M$） - 任意两城市之间连通 - $1 \leq C_i \leq 10^9$ （$1 \leq i \leq N$） - $1 \leq R_i \leq 10$ （$1 \leq i \leq N$） - 所有输入均为整数。 由 ChatGPT 5 翻译