AT_pakencamp_2024_day1_p Bombard

有一个高 $H$ 行、宽 $W$ 列的网格。我们将左上角的格子记作 $(1, 1)$，从上往下的第 $x$ 行、从左往右的第 $y$ 列的格子记作 $(x, y)$。 在这个网格上，建立了 $N$ 个矩形结构物。第 $i$ 个结构物覆盖所有满足 $U_i \leq x \leq D_i,\;L_i \leq y \leq R_i$ 的格子 $(x, y)$，并且不覆盖其他格子。保证每一个格子至多被一个结构物覆盖。每个结构物都有一个值 $C_i$。 每个格子的价值定义为覆盖它的结构物的值。如果没有结构物覆盖该格子，则该格子的价值为 $0$。 Falcon 君持有一门波动炮，可以从某个位置向右摧毁所有的格子。具体来说，如果在格子 $(x, y)$ 发射波动炮，则对于所有满足 $y \leq j \leq W$ 的整数 $j$，格子 $(x, j)$ 都会被摧毁。 这时，Falcon 君的“开心值”即为被摧毁的所有格子的价值之和。 波动炮可以在上下方向随意移动，但不能左右移动。现在给定 $Q$ 个需要考虑的候选发射列，对于第 $K_i$ 列，请求出 Falcon 君的最大“开心值”。

输入通过标准输入以以下格式给出。 > $N\ H\ W$ > $U_1\ D_1\ L_1\ R_1\ C_1$ > $U_2\ D_2\ L_2\ R_2\ C_2$ > $\vdots$ > $U_N\ D_N\ L_N\ R_N\ C_N$ > $Q$ > $K_1$ > $K_2$ > $\vdots$ > $K_Q$

请输出答案。

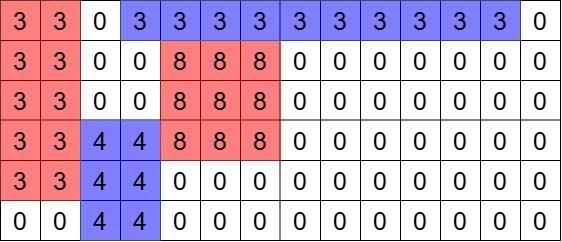
### 样例解释 1 网格如下图所示。  例如，从第 $1$ 列发射时： - 放在第 $1$ 行时，开心值为 $36$； - 放在第 $2$ 行时，开心值为 $30$； - 放在第 $3$ 行时，开心值为 $30$； - 放在第 $4$ 行时，开心值为 $38$； - 放在第 $5$ 行时，开心值为 $14$； - 放在第 $6$ 行时，开心值为 $8$。 因此，需要输出 $38$。 ### 数据范围 - $1 \leq N \leq 10^5$ - $1 \leq H,W \leq 10^9$ - $1 \leq U_i \leq D_i \leq H$（$1 \leq i \leq N$） - $1 \leq L_i \leq R_i \leq W$（$1 \leq i \leq N$） - 不存在两个结构物覆盖同一格子 - $1 \leq C_i \leq 10^9$（$1 \leq i \leq N$） - $1 \leq Q \leq 2 \times 10^5$ - $1 \leq K_i \leq W$（$1 \leq i \leq Q$） - 所有输入均为整数。 由 ChatGPT 5 翻译