AT_pakencamp_2024_day2_c Can Make Palindrome

パ研王国由 $N$ 个城镇组成，每个城镇分别编号为 $1, 2, \ldots, N$。这些城镇通过 $N-1$ 条道路相连，道路编号为 $1, 2, \ldots, N-1$。第 $i$ 条道路（$1 \leq i \leq N-1$）双向连接着城镇 $A_i$ 和城镇 $B_i$。任意两个城镇之间都可以通过若干（包括零）条道路相互到达。 定义两个城镇 $a, b$ 之间的距离为从 $a$ 走到 $b$ 时所经过的最少边数。特别地，当 $a=b$ 时，距离为 $0$。 每个城镇都有一家出售“文字”的商店。パ研王国的“文字”用区间 $[1, N]$ 内的整数表示，城镇 $i$ 的商店只出售文字 $C_i$。且每家商店的库存都足够，不会卖光。 接下来，パ研王国将连续举办 $M$ 天的游行活动。第 $i$ 天，沿从城镇 $U_i$ 到城镇 $V_i$ 的最短路径上的所有城镇（包括 $U_i, V_i$）都会举办游行。特别地，若 $U_i = V_i$，那么仅在该城镇举办。当天，仅有游行路线上的城镇商店开门营业，其他城镇的商店关闭，无法购买文字。 作为パ研王国的国王，你希望用由各地居民献上的文字，迎接前来参加游行的民众。你会在第 $i$ 天向居住在编号为 $L_i, L_i+1, \ldots, R_i$ 的城镇的居民分别下达如下指示： - 第 $i$ 天，居住在指定区间内每个城镇的居民，各自从距离自己最近的游行城镇的商店购买一种文字，然后献给你。 你相信回文字符串最为美丽，因此想用居民们献上的文字制作回文以示欢迎。给出 $Q$ 个区间 $(S_i, T_i)$，请判断在重新排列 $S_i, S_i+1, \ldots, T_i$ 天获得的所有文字后，是否能组成一个回文串。

输入按如下格式从标准输入中给出： > $N$ > $A_1$ $B_1$ > $A_2$ $B_2$ > $\vdots$ > $A_{N-1}$ $B_{N-1}$ > $C_1$ $C_2$ $\ldots$ $C_N$ > $M$ > $U_1$ $V_1$ $L_1$ $R_1$ > $U_2$ $V_2$ $L_2$ $R_2$ > $\vdots$ > $U_M$ $V_M$ $L_M$ $R_M$ > $Q$ > $S_1$ $T_1$ > $S_2$ $T_2$ > $\vdots$ > $S_Q$ $T_Q$

输出 $Q$ 行。对于每组整数对 $(S_i, T_i)$，如果通过重新排列这段时间获得的全部文字可以构成回文串，则输出 `Yes`，否则输出 `No`。（12:51 修正）

## 小子任务 1. （$5$ 分）$N \leq 300, M \leq 300, Q = 1, S_1 = 1, T_1 = M, C_i \leq 2$（$1 \leq i \leq N$） 2. （$5$ 分）$N \leq 2000, M \leq 2000, Q = 1, S_1 = 1, T_1 = M, C_i \leq 2$（$1 \leq i \leq N$） 3. （$5$ 分）$N \leq 2000, M \leq 2000, C_i \leq 2$（$1 \leq i \leq N$） 4. （$5$ 分）$A_i = i, B_i = i+1$（$1 \leq i \leq N-1$），$C_i \leq 2$（$1 \leq i \leq N$） 5. （$20$ 分）$A_{i+1} = B_i$（$1 \leq i \leq N-2$），$C_i \leq 2$（$1 \leq i \leq N$） 6. （$10$ 分）$A_{i+1} = B_i$（$1 \leq i \leq N-2$） 7. （$40$ 分）$C_i \leq 2$（$1 \leq i \leq N$） 8. 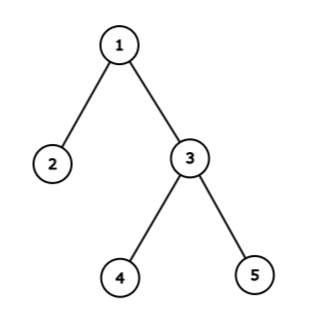（$10$ 分）无额外限制 ## 样例解释 1 パ研王国如图所示：  此外，每天游行发生如下： - 第 $1$ 天在城镇 $1, 3, 5$ 举行。你会对城镇 $2, 3, 4$ 的居民下指示，居民分别在城镇 $1, 3, 3$ 购得文字 $1, 1, 1$。 - 第 $2$ 天在城镇 $2, 1, 3, 4$ 举行。你会对城镇 $1, 2, 3$ 的居民下指示，居民分别在城镇 $1, 2, 3$ 购得文字 $1, 2, 1$。 - 第 $3$ 天在城镇 $3$ 举行。你会对城镇 $5$ 的居民下指示，居民在城镇 $3$ 获得文字 $1$。 于是，第 $1, 2, 3$ 天获得的全部文字重排可组成 $1, 1, 1, 2, 1, 1, 1$，可以排列成回文。 本样例满足小题 $1, 2, 3, 7, 8$ 的限制。 ## 样例解释 2 本样例满足小题 $3, 4, 5, 6, 7, 8$ 的限制。 ## 样例解释 3 本样例满足小题 $3, 5, 6, 7, 8$ 的限制。 ## 样例解释 4 本样例满足小题 $8$ 的限制。 ## 数据范围 - $2 \leq N \leq 2 \times 10^5$ - $1 \leq M \leq 2 \times 10^5$ - $1 \leq Q \leq 2 \times 10^5$ - $1 \leq A_i, B_i \leq N$（$1 \leq i \leq N-1$） - 任意两城镇间均连通 - $1 \leq C_i \leq N$（$1 \leq i \leq N$） - $1 \leq U_i \leq V_i \leq N$（$1 \leq i \leq M$） - $1 \leq L_i \leq R_i \leq N$（$1 \leq i \leq M$） - $1 \leq S_i \leq T_i \leq M$（$1 \leq i \leq Q$） - 输入均为整数 由 ChatGPT 5 翻译