AT_pakencamp_2024_day2_c Can Make Palindrome

パ研王国は $ N $ 個の町からなり、それぞれの町には $ 1, 2, \ldots, N $ の番号が付いています。これらの町は $ N-1 $ 個の道路で結ばれており、道路には $ 1, 2, \ldots, N-1 $ の番号が付いています。道路 $ i $ $ (1 \leq i \leq N-1) $ は町 $ A_i $ と町 $ B_i $ を双方向に結んでいます。どの町からどの町へも $ 0 $ 本以上の道路を通り移動できます。 $ 2 $ つの町 $ a, b $ の距離を、 $ a $ から $ b $ に移動するときに通る辺の個数の最小値とします。特に、 $ a=b $ のとき、距離は $ 0 $ であることに注意してください。 パ研王国のそれぞれの町には、文字を売る店があります。パ研王国の文字は $ 1 $ 以上 $ N $ 以下の整数で表され、町 $ i $ にある店では文字 $ C_i $ のみを買うことができます。それぞれの店には十分な在庫があり、売り切れることはないものとします。 さて、パ研王国ではこれから $ M $ 日間に渡りパレードが開催されます。 $ i $ 日目には、町 $ U_i $ から町 $ V_i $ へ移動する最短経路上にある町(町 $ U_i, V_i $ を含む)がパレードの開催される町となります。特に、 $ U_i = V_i $ のとき、パレードは町 $ U_i $ でのみ開催されます。パレードの開催される町の店は営業しており、文字を買うことができますが、それ以外の町にある店は全て閉じてしまい、文字を買うことができません。 パ研王国の王様であるあなたは、パレードを見に来た人たちに歓迎の意を伝えるため、 $ M $ 日間にわたり国民に指示を出します。 $ i $ 日目には、町 $ L_i, L_i+1, \ldots, R_i $ に住む住民それぞれ $ 1 $ 人に対し、次のような指示を出します。 - $ i $ 日目にパレードの開催される町のうち、その国民の住む町からの距離が最も小さい町の店で文字を買い、あなたに献上する。 回文こそが最も美しい文字列であると信じるあなたは、指示により献上される文字を用いて作った回文を飾ることで歓迎の意を伝えようと思っています。 $ Q $ 個の整数組 $ (S_i, T_i) $ が与えられるので、 $ S_i, S_i+1, \ldots, T_i $ 日目に献上される文字を全て用い、適切に並び替えることで、回文を作ることができるかを判定してください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_{N-1} $ $ B_{N-1} $ $ C_1 $ $ C_2 $ $ \ldots $ $ C_N $ $ M $ $ U_1 $ $ V_1 $ $ L_1 $ $ R_1 $ $ U_2 $ $ V_2 $ $ L_2 $ $ R_2 $ $ \vdots $ $ U_M $ $ V_M $ $ L_M $ $ R_M $ $ Q $ $ S_1 $ $ T_1 $ $ S_2 $ $ T_2 $ $ \vdots $ $ S_Q $ $ T_Q $

$ Q $ 行出力せよ。 $ i $ 行目には $ i $ 番目の整数組 $ (S_i, T_i) $ について、回文を作ることができるならば `Yes` を、できないならば `No` を出力せよ。 (12:51 修正)

### 小課題 1. ( $ 5 $ 点) $ N \leq 300, M \leq 300, Q = 1, S_1 = 1, T_1 = M, C_i \leq 2 $ ( $ 1 \leq i \leq N $ ) 2. ( $ 5 $ 点) $ N \leq 2000, M \leq 2000, Q = 1, S_1 = 1, T_1 = M, C_i \leq 2 $ ( $ 1 \leq i \leq N $ ) 3. ( $ 5 $ 点) $ N \leq 2000, M \leq 2000, C_i \leq 2 $ ( $ 1 \leq i \leq N $ ) 4. ( $ 5 $ 点) $ A_i=i, B_i=i+1 $ ( $ 1 \leq i \leq N-1 $ ) $ ,C_i \leq 2 $ ( $ 1 \leq i \leq N $ ) 5. ( $ 20 $ 点) $ A_{i+1} = B_i $ ( $ 1 \leq i \leq N-2 $ ) $ ,C_i \leq 2 $ ( $ 1 \leq i \leq N $ ) 6. ( $ 10 $ 点) $ A_{i+1} = B_i $ ( $ 1 \leq i \leq N-2 $ ) 7. ( $ 40 $ 点) $ C_i \leq 2 $ ( $ 1 \leq i \leq N $ ) 8. ( $ 10 $ 点) 追加の制約はない ### Sample Explanation 1 パ研王国は以下のようになります。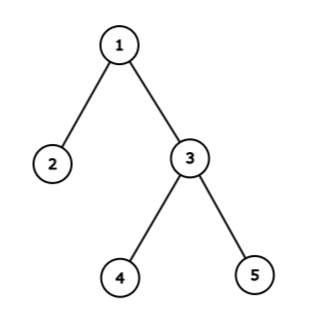  また、各日には次のような出来事が起こります。 - $ 1 $ 日目は町 $ 1, 3, 5 $ でパレードが開催されます。あなたは町 $ 2, 3, 4 $ の住人に指示を出し、住人はそれぞれ町 $ 1, 3, 3 $ で文字 $ 1, 1, 1 $ を買います。 - $ 2 $ 日目は町 $ 2, 1, 3, 4 $ でパレードが開催されます。あなたは町 $ 1, 2, 3 $ の住人に指示を出し、住人はそれぞれ町 $ 1, 2, 3 $ で文字 $ 1, 2, 1 $ を買います。 - $ 3 $ 日目は町 $ 3 $ でパレードが開催されます。あなたは町 $ 5 $ の住人に指示を出し、住人はそれぞれ町 $ 3 $ で文字 $ 1 $ を買います。 よって、 $ 1, 2, 3 $ 日目に献上される文字を並び替えると、 $ 1, 1, 1, 2, 1, 1, 1 $ という回文を作ることができます。 この入力例は小課題 $ 1, 2, 3, 7, 8 $ の制約を満たします。 ### Sample Explanation 2 この入力例は小課題 $ 3, 4, 5, 6, 7, 8 $ の制約を満たします。 ### Sample Explanation 3 この入力例は小課題 $ 3, 5, 6, 7, 8 $ の制約を満たします。 ### Sample Explanation 4 この入力例は小課題 $ 8 $ の制約を満たします。 ### Constraints - $ 2 \leq N \leq 2 \times 10^5 $ - $ 1 \leq M \leq 2 \times 10^5 $ - $ 1 \leq Q \leq 2 \times 10^5 $ - $ 1 \leq A_i, B_i \leq N $ ( $ 1 \leq i \leq N-1 $ ) - どの町からどの町へも $ 0 $ 本以上の道路を通り移動できる - $ 1 \leq C_i \leq N $ ( $ 1 \leq i \leq N $ ) - $ 1 \leq U_i \leq V_i \leq N $ ( $ 1 \leq i \leq M $ ) - $ 1 \leq L_i \leq R_i \leq N $ ( $ 1 \leq i \leq M $ ) - $ 1 \leq S_i \leq T_i \leq M $ ( $ 1 \leq i \leq Q $ ) - 入力は全て整数