AT_panasonic2020_b Bishop
题目描述
有一个高 $H$ 行、宽 $W$ 列的棋盘。在这个棋盘的左上角格子上放置了一枚角行棋子。请问,这枚棋子经过 $0$ 次或多次任意移动后,最多能到达多少个格子?
其中,角行棋子只能沿对角线方向移动。更严格地说,若棋子当前在从上往下第 $r_1$ 行、从左往右第 $c_1$ 列的格子上,能移动到从上往下第 $r_2$ 行、从左往右第 $c_2$ 列的格子的条件是:
- $r_1 + c_1 = r_2 + c_2$
- $r_1 - c_1 = r_2 - c_2$
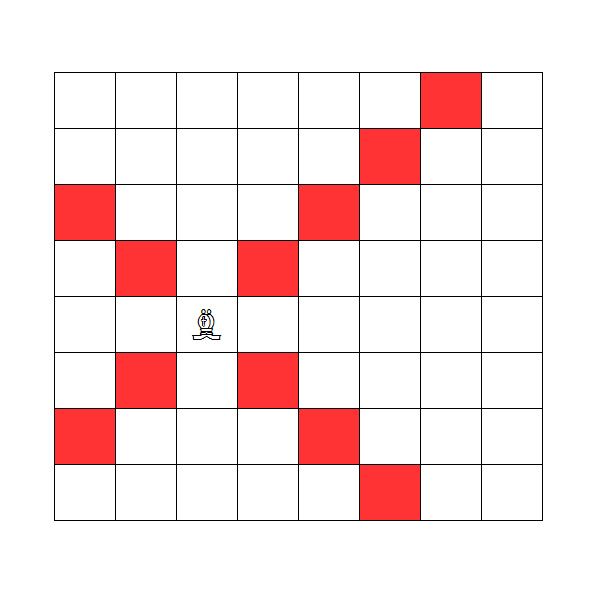
上述两个条件中,恰好有一个成立时,棋子可以移动。例如,当棋子处于图中的位置时,一次移动可以到达红色标记的格子。
输入格式
输入从标准输入读入,格式如下:
> $H\ W$
输出格式
输出棋子能够到达的格子的总数。
说明/提示
## 限制条件
- $1 \leq H, W \leq 10^9$
- 输入均为整数。
## 样例解释 1
下图中水色的格子为可到达的格子。
## 样例解释 2
下图中水色的格子为可到达的格子。
由 ChatGPT 4.1 翻译