AT_panasonic2020_b Bishop

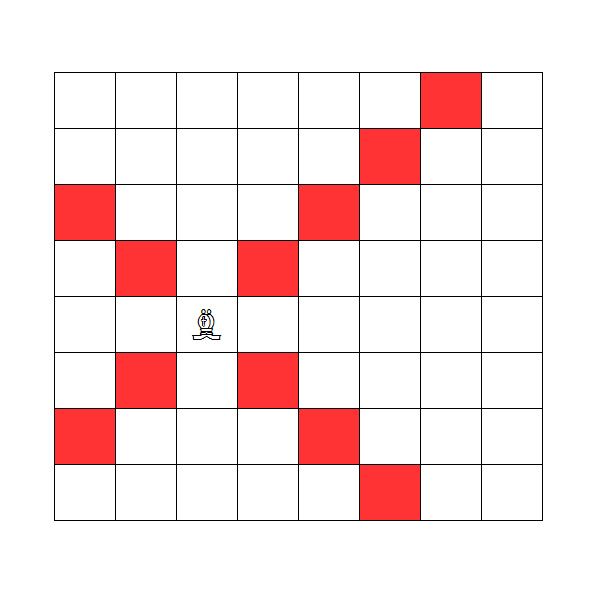
[problemUrl]: https://atcoder.jp/contests/panasonic2020/tasks/panasonic2020_b 縦 $ H $ マス、横 $ W $ マスの盤面があります。 この盤面の左上隅のマスに角行の駒が置かれています。 駒が $ 0 $ 回以上の好きな回数の移動を繰り返して到達できるマス目は何個あるでしょうか？ ただし、角行の駒は斜めに動くものとします。 より厳密には、駒が上から $ r_1 $ 番目、左から $ c_1 $ 番目のマスから上から $ r_2 $ 番目、左から $ c_2 $ 番目のマス目に動ける条件は - $ r_1\ +\ c_1\ =\ r_2\ +\ c_2 $ - $ r_1\ -\ c_1\ =\ r_2\ -\ c_2 $ のうちちょうど一方が成立することです。たとえば、駒が図の位置にあるとき、一回で移動できる場所は赤くなっているマスです。 

入力は以下の形式で標準入力から与えられる。 > $ H\ W $

駒が到達できるマス目の個数を出力せよ。

### 制約 - $ 1\ \leq\ H,\ W\ \leq\ 10^9 $ - 入力は全て整数である。 ### Sample Explanation 1 下図の水色のマスに到達可能です。 !\[\](https://img.atcoder.jp/panasonic2020/b218e01560fe6e40e7d082ca57a64e6e.png) ### Sample Explanation 2 下図の水色のマスに到達可能です。 !\[\](https://img.atcoder.jp/panasonic2020/088830f8a244d99a9f95d20bf9a8d336.png)