AT_panasonic2020_f Fractal Shortest Path
题目描述
对于非负整数 $K$,定义如下的 $K$ 级分形图案。
- $0$ 级分形是仅包含一个白色格子的网格。
- 当 $K > 0$ 时,$K$ 级分形是一个 $3^K \times 3^K$ 的网格。将该网格划分为 $9$ 个 $3^{K-1} \times 3^{K-1}$ 的子块时,
- 中央的子块全部为黑色格子。
- 其余 $8$ 个子块均为 $K-1$ 级分形。
例如,$2$ 级分形如下图所示。
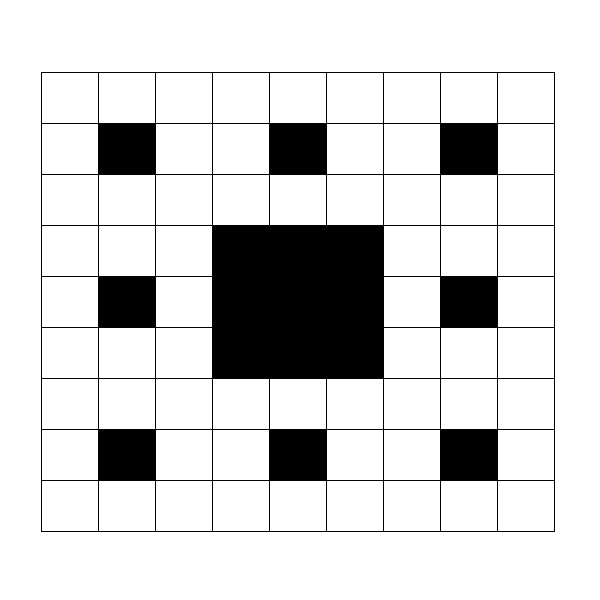
在 $30$ 级分形中,将从上往下第 $r$ 行,从左往右第 $c$ 列的格子记作 $(r, c)$。
给定 $Q$ 组整数 $(a_i, b_i, c_i, d_i)$,对于每组,求从 $(a_i, b_i)$ 到 $(c_i, d_i)$ 的距离。
这里,从 $(a, b)$ 到 $(c, d)$ 的距离定义为满足以下条件的最小 $n$:
- 存在一条仅经过白色格子的路径 $(x_0, y_0), \ldots, (x_n, y_n)$,满足:
- $(x_0, y_0) = (a, b)$
- $(x_n, y_n) = (c, d)$
- 对于任意 $i$($0 \leq i \leq n-1$),格子 $(x_i, y_i)$ 与 $(x_{i+1}, y_{i+1})$ 边相邻。
输入格式
输入从标准输入读入,格式如下:
> $Q$
> $a_1\ b_1\ c_1\ d_1$
> $\vdots$
> $a_Q\ b_Q\ c_Q\ d_Q$
输出格式
输出共 $Q$ 行。第 $i$ 行输出从 $(a_i, b_i)$ 到 $(c_i, d_i)$ 的距离。
说明/提示
### 数据范围
- $1 \leq Q \leq 10000$
- $1 \leq a_i, b_i, c_i, d_i \leq 3^{30}$
- $(a_i, b_i) \neq (c_i, d_i)$
- $(a_i, b_i)$ 和 $(c_i, d_i)$ 均为白色格子
- 输入均为整数
### 样例解释 1

由 ChatGPT 4.1 翻译