AT_panasonic2020_f Fractal Shortest Path

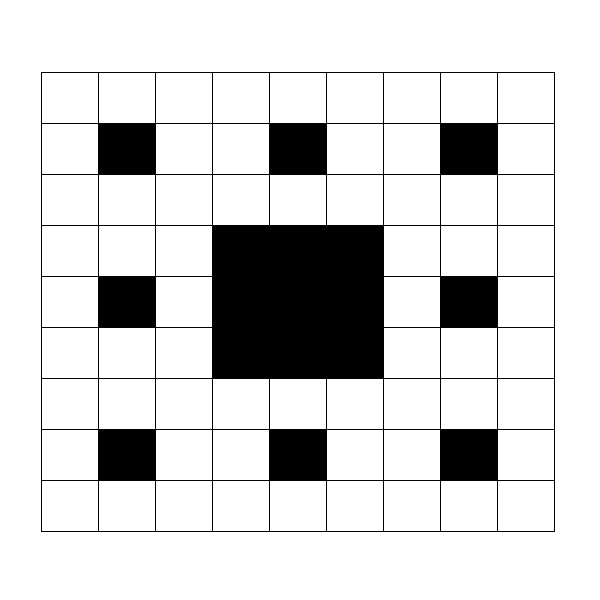
[problemUrl]: https://atcoder.jp/contests/panasonic2020/tasks/panasonic2020_f 非負整数 $ K $ に対し、以下のようにレベル $ K $ のフラクタルを定義します。 - レベル $ 0 $ のフラクタルとは、白いマス一個のみからなるグリッドである。 - $ K\ >\ 0 $ のとき、レベル $ K $ のフラクタルは $ 3^K\ \times\ 3^K $ のグリッドである。このグリッドを $ 3^{K-1}\ \times\ 3^{K-1} $ のブロック $ 9 $ 個に分割したとき、 - 中央のブロックは全て黒マスからなる。 - 他の $ 8 $ 個のブロックは、レベル $ K-1 $ のフラクタルになっている。 たとえば、レベル $ 2 $ のフラクタルは下図の通りです。  レベル $ 30 $ のフラクタルにおいて、上から $ r $ 番目、左から $ c $ 番目のマスを $ (r,\ c) $ と書きます。 $ Q $ 個の整数組 $ (a_i,\ b_i,\ c_i,\ d_i) $ が与えられます。 それぞれの組について、$ (a_i,\ b_i) $ から $ (c_i,\ d_i) $ への距離を求めてください。 ただし、$ (a,\ b) $ から $ (c,\ d) $ への距離とは、以下の条件を満たすような最小の $ n $ とします。 - ある白マスの列 $ (x_0,\ y_0),\ \ldots,\ (x_n,\ y_n) $ が存在して、以下の条件を満たす。 - $ (x_0,\ y_0)\ =\ (a,\ b) $ - $ (x_n,\ y_n)\ =\ (c,\ d) $ - 任意の $ i\ (0\ \leq\ i\ \leq\ n-1) $ に対し、マス $ (x_i,\ y_i) $ と $ (x_{i+1},\ y_{i+1}) $ は辺で接する。

入力は以下の形式で標準入力から与えられる。 > $ Q $ $ a_1\ b_1\ c_1\ d_1 $ $ : $ $ a_Q\ b_Q\ c_Q\ d_Q $

$ Q $ 行出力せよ。 $ i $ 行目には、$ (a_i,\ b_i) $ から $ (c_i,\ d_i) $ への距離を出力せよ。

### 制約 - $ 1\ \leq\ Q\ \leq\ 10000 $ - $ 1\ \leq\ a_i,\ b_i,\ c_i,\ d_i\ \leq\ 3^{30} $ - $ (a_i,\ b_i)\ \neq\ (c_i,\ d_i) $ - $ (a_i,\ b_i),\ (c_i,\ d_i) $ は白マスである。 - 入力は全て整数である。 ### Sample Explanation 1 !\[\](https://img.atcoder.jp/panasonic2020/b590cee9850abdad4109ab940f9efe5a.png)