AT_past18_i 改行コード

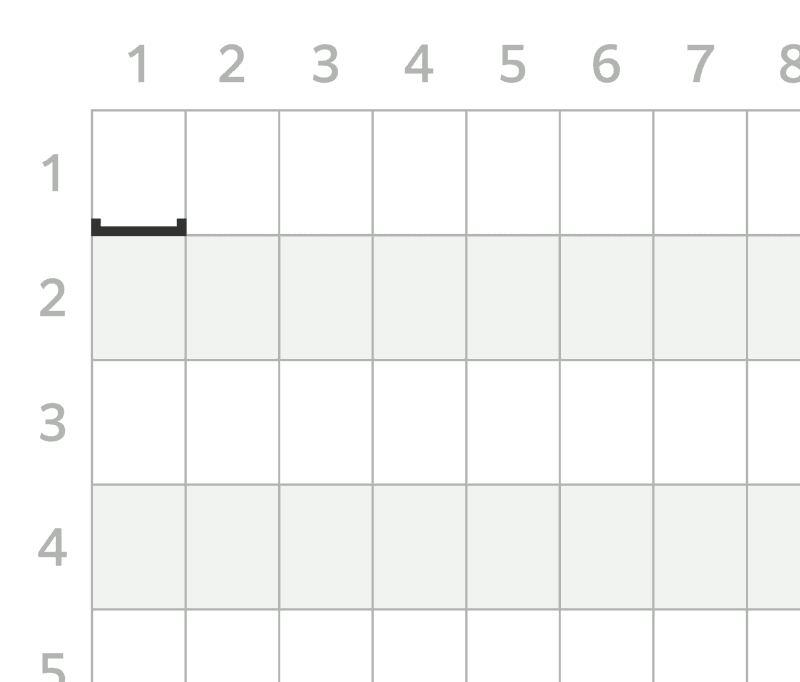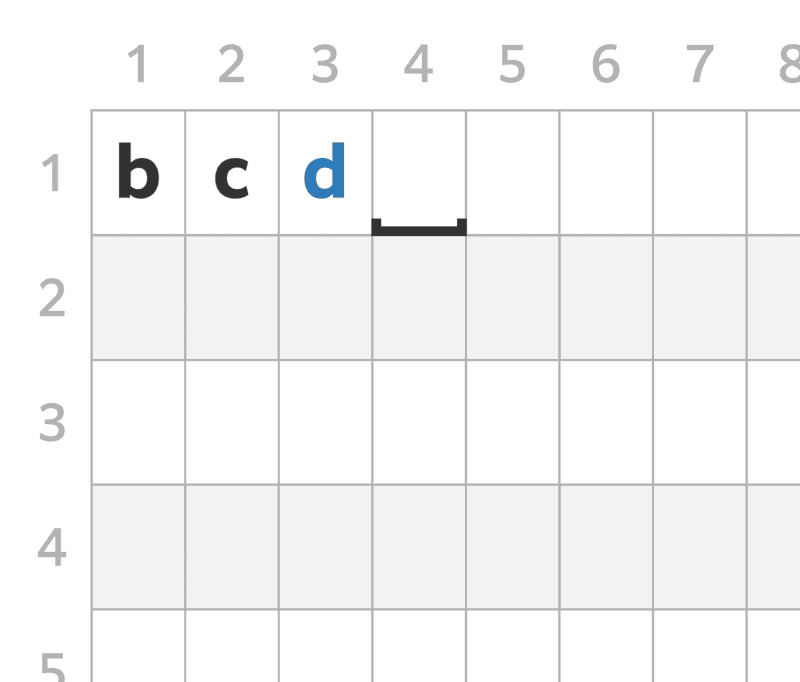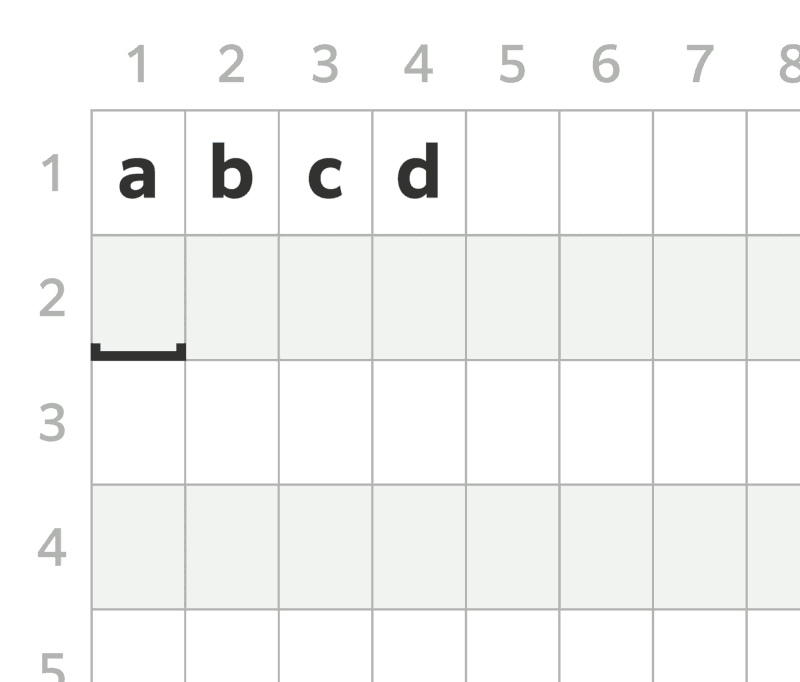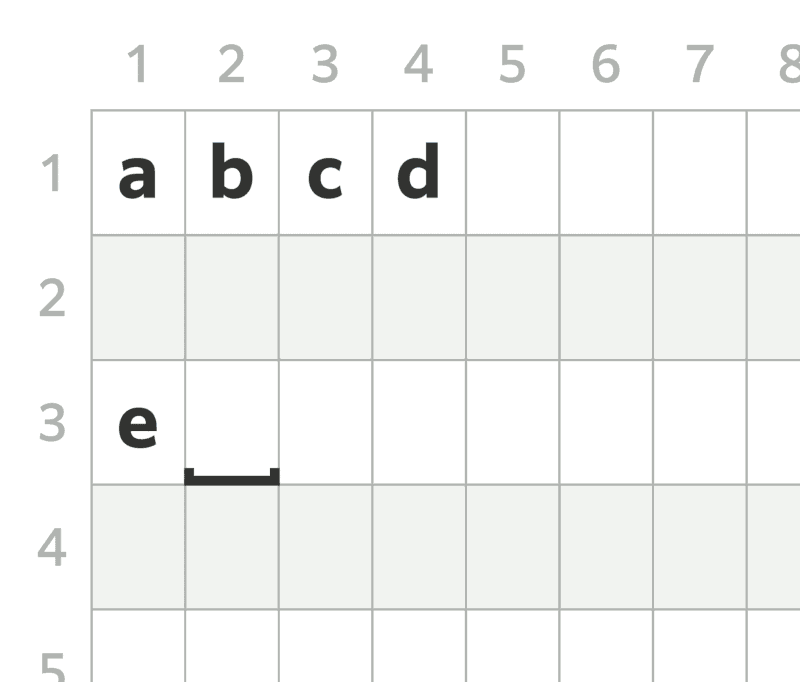
There is a text editor that can be regarded as a grid extending infinitely toward right and downward. The cell in the $ i $ -th row from the top and $ j $ -th column from the left of the editor is denoted by $ (i, j) $ . Each cell can have a character written on it, or be empty; initially, all cells are empty. The editor also has a marker called a **cursor**, which indicates the position where a character is inserted. The cursor is initially located at $ (1, 1) $ . You are to process $ Q $ queries in given order. Each query is one of the following three types. - $ 1 $ $ c $ : Insert the character $ c $ at the current position of the cursor. Formally, perform the following procedure. - First, move all characters in the current cell of the cursor or in any cell to the right within the same row, one cell to the right, if any. - Next, write the character $ c $ onto the cell where the cursor is currently located at. - Finally, move the cursor one cell to the right. - $ 2 $ : Move the cursor to the leftmost cell of the current row. - $ 3 $ : Move the cursor to the leftmost cell of the row right below the current row. Print the state of the editor after processing all the queries.

The input is given from Standard Input in the following format, where $ \mathrm{query}_i $ denotes the $ i $ -th query: > $ Q $ $ \mathrm{query}_1 $ $ \mathrm{query}_2 $ $ \vdots $ $ \mathrm{query}_Q $

- Let cell $ (H, W) $ be the position of the cursor when all the queries are processed. - Let $ C_i $ be the number of characters in the $ i $ -th row from the top. - Let $ S_{i, j} $ be the character written on cell $ (i, j) $ . Print $ (H+1) $ lines in the following format. (Note that $ C_i = 0 $ may apply for some rows.) Beware that the second and succeeding lines must be preceded by `#` and a space. > $ H $ $ W $ \# $ S_{1, 1}S_{1, 2} \dots S_{1, C_1} $ \# $ S_{2, 1}S_{2, 2} \dots S_{2, C_2} $ $ \vdots $ \# $ S_{H, 1}S_{H, 2} \dots S_{H, C_H} $

### Sample Explanation 1 The query is processed as follows. - In the $ 1 $ -st query, write `b` onto $ (1, 1) $ , and move the cursor to $ (1, 2) $ . - In the $ 2 $ -nd query, write `c` onto $ (1, 2) $ , and move the cursor to $ (1, 3) $ . - In the $ 3 $ -rd query, write `d` onto $ (1, 3) $ , and move the cursor to $ (1, 4) $ . - In the $ 4 $ -th query, move the cursor to $ (1, 1) $ . - In the $ 5 $ -th query, simultaneously move the following characters one cell to the right: `b` written on $ (1, 1) $ , `c` written on $ (1, 2) $ , and `d` written on $ (1, 3) $ . Then, write `a` onto $ (1, 1) $ , and move the cursor to $ (1, 2) $ . - In the $ 6 $ -th query, move the cursor to $ (2, 1) $ . - In the $ 7 $ -th query, move the cursor to $ (3, 1) $ . - In the $ 8 $ -th query, write `e` onto $ (3, 1) $ , and move the cursor to $ (3, 2) $ .  ### Constraints - $ 1 \leq Q \leq 1.5 \times 10^6 $ - $ c $ is a lowercase English character.