AT_past19_i 道の沈没

AtCoderLand has $ N $ islands: island $ 1 $ , island $ 2 $ , $ \ldots $ , and island $ N $ , and $ M $ roads: road $ 1 $ , road $ 2 $ , $ \ldots $ , and road $ M $ . Road $ i $ connects island $ A_i $ and island $ B_i $ bidirectionally. Road $ i\ (1\leq i\leq M) $ will be submerged on day $ D_i $ , so it will not be available on or after day $ D_i $ . The islands are said to be connected if one can travel between any pair of islands via available roads. On day $ 0 $ (when no road is submerged), the islands are connected. Find the integer $ X $ such that the islands are connected on day $ (X-1) $ but not on day $ X $ .

The input is given from Standard Input in the following format: > $ N $ $ M $ $ A _ 1 $ $ B _ 1 $ $ D _ 1 $ $ A _ 2 $ $ B _ 2 $ $ D _ 2 $ $ \vdots $ $ A _ M $ $ B _ M $ $ D _ M $

Print the answer.

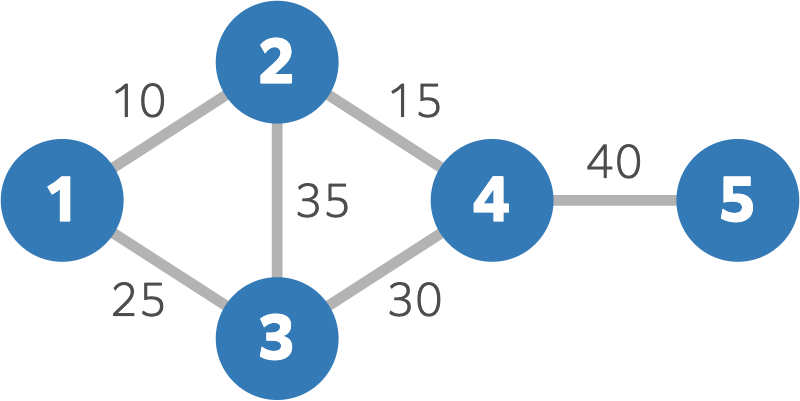
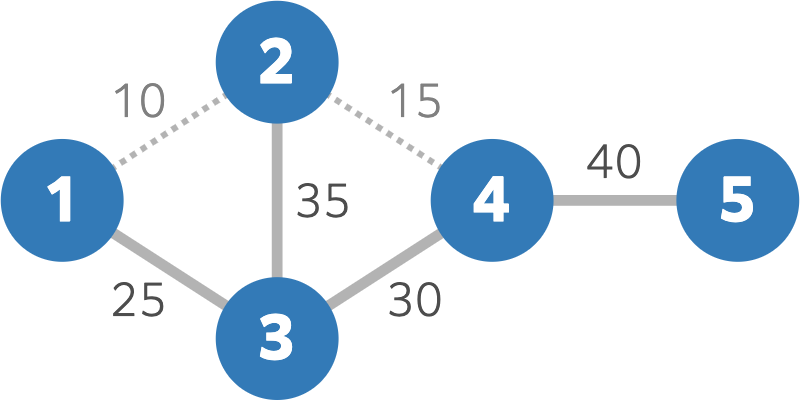
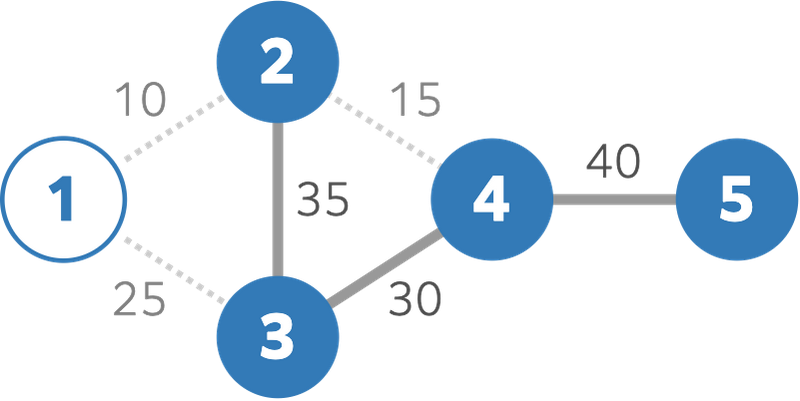
### Sample Explanation 1 The islands of AtCoderLand are illustrated in the figure below:  On day $ 24 $ , the islands are connected.  On day $ 25 $ , road $ 2 $ will be submerged, making it impossible to travel between, for instance, island $ 1 $ and island $ 2 $ .  Thus, $ 25 $ should be printed. ### Sample Explanation 2 There may be a road that leads from an island to itself, or multiple roads between the same pair of islands. ### Constraints - $ 2\leq N\leq2\times10 ^ 5 $ - $ N-1\leq M\leq2\times10 ^ 5 $ - $ 1\leq A _ i\leq B _ i\leq N\ (1\leq i\leq M) $ - $ 1\leq D _ i\leq10 ^ 9\ (1\leq i\leq M) $ - The islands are initially connected. - All input values are integers.