AT_past19_i 道の沈没

AtCoder 国には島 $ 1, $ 島 $ 2,\ldots, $ 島 $ N $ の $ N $ 個の島があります。 また、AtCoder 国には道 $ 1, $ 道 $ 2,\ldots, $ 道 $ M $ の $ M $ 本の道があり、道 $ i $ は島 $ A _ i $ と島 $ B _ i $ を双方向に結んでいます。 道 $ i\ (1\leq i\leq M) $ は $ D _ i $ 日に沈んでしまうため、 $ D _ i $ 日以降に道 $ i $ を利用することはできません（ $ D _ i $ 日にも利用できません）。 どの $ 2 $ つの島もいくつかの利用可能な道を使って行き来できることを、すべての島が連結であるということにします。 $ 0 $ 日には（つまり、どの道も沈んでいないときには）、すべての島は連結です。 $ X-1 $ 日にはすべての島が連結であるが、 $ X $ 日にはそうでないような整数 $ X $ を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ A _ 1 $ $ B _ 1 $ $ D _ 1 $ $ A _ 2 $ $ B _ 2 $ $ D _ 2 $ $ \vdots $ $ A _ M $ $ B _ M $ $ D _ M $

答えを出力せよ。

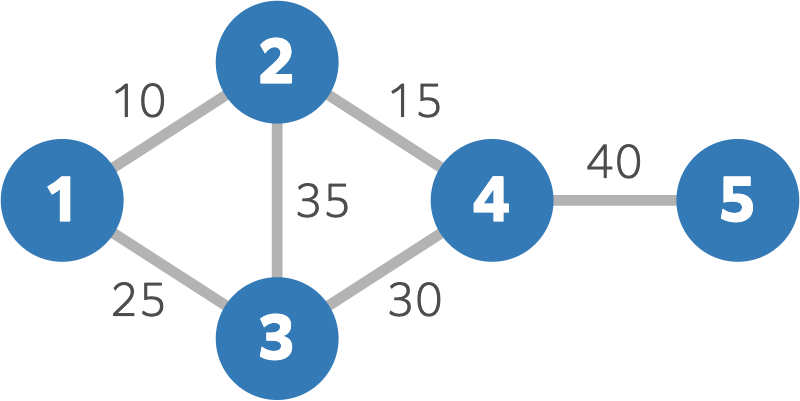
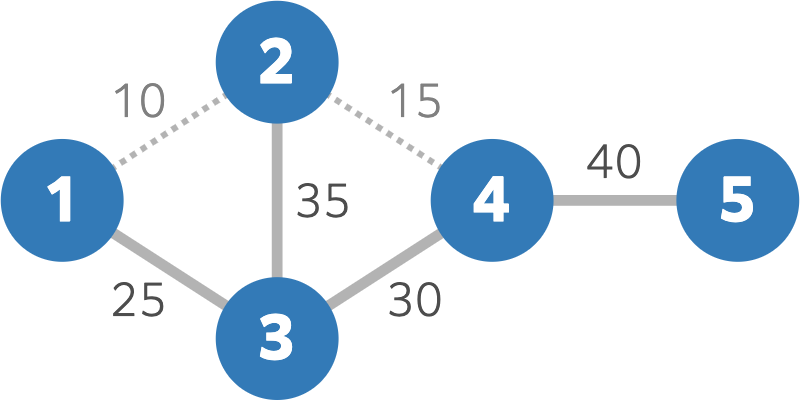
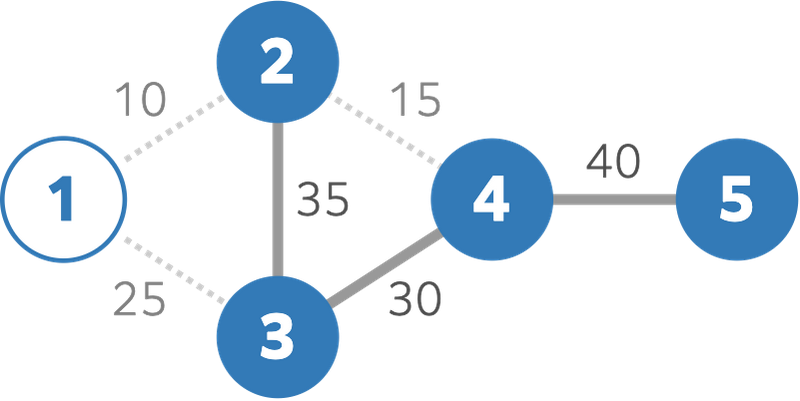
### Sample Explanation 1 AtCoder 国の島は以下の図のようになっています。  $ 24 $ 日には、すべての島が連結です。  $ 25 $ 日には道 $ 2 $ が沈み、たとえば島 $ 1 $ と島 $ 2 $ を行き来することができなくなります。  よって、 $ 25 $ を出力してください。 ### Sample Explanation 2 同じ島へ戻ってくる道や、全く同じ島どうしを結んでいる複数の道がある場合もあります。 ### Constraints - $ 2\leq N\leq2\times10 ^ 5 $ - $ N-1\leq M\leq2\times10 ^ 5 $ - $ 1\leq A _ i\leq B _ i\leq N\ (1\leq i\leq M) $ - $ 1\leq D _ i\leq10 ^ 9\ (1\leq i\leq M) $ - はじめ、すべての島は連結 - 入力はすべて整数