AT_qupc2014_d 切符分割

[problemUrl]: https://atcoder.jp/contests/qupc2014/tasks/qupc2014_d QU鉄道は、$ N $個の駅と$ M $個の路線を持つ鉄道会社である。 それぞれの駅には、$ 0 $から$ N-1 $までの一意な駅番号が割り当てられている。 各路線は異なる$ 2 $つの駅を結んでおり、どちらの方向の移動にも使うことができる。 また、QU鉄道では運賃表を使用しており、距離に応じて段階的に運賃が変わるようになっている。 ある駅Aから別の駅Bまでの切符の料金は、駅Aから駅Bまでの最短距離を元に、運賃表から決定する。 例えば、次のような路線図と運賃表を考えよう。  距離運賃$ 1 $ km - $ 6 $ km$ 180 $ 円$ 7 $ km - $ 15 $ km$ 230 $ 円$ 16 $ km - $ 25 $ km$ 400 $ 円$ 26 $ km - $ 40 $ km$ 530 $ 円$ 41 $ km - $ 60 $ km$ 740 $ 円$ 61 $ km以上$ 820 $ 円 この例において、駅$ 0 $から駅$ 6 $までの運賃を考えよう。 駅$ 0 $から駅$ 6 $までの距離は合計で$ 41 $kmであるから、 運賃表より、駅$ 0 $から駅$ 6 $までの切符は$ 740 $円となる。 QU鉄道では、区間の異なる複数の切符を使って、ある駅から別の駅へ移動することもできる。 これを切符分割と呼ぶことにする。 例えば、次の$ 2 $つの切符を持っていれば、駅$ 0 $から駅$ 6 $まで移動することができる。 - 駅$ 0 $から駅$ 1 $までの切符： $ 6 $km、$ 180 $円 - 駅$ 1 $から駅$ 6 $までの切符： $ 35 $km、$ 530 $円 このときの運賃の合計は$ 180+530=710 $円となり、 駅$ 0 $から駅$ 6 $までの切符$ 1 $枚を買う場合と比べて安くなる。 このように、QU鉄道では、切符分割により運賃が安くなる場合が存在する。 さらに、次のように$ 3 $枚の切符を使って、駅$ 0 $から駅$ 6 $まで移動する場合を考える。 - 駅$ 0 $から駅$ 2 $までの切符： $ 13 $km、$ 230 $円 - 駅$ 2 $から駅$ 4 $までの切符： $ 14 $km、$ 230 $円 - 駅$ 4 $から駅$ 6 $までの切符： $ 14 $km、$ 230 $円 このときの運賃の合計は$ 230+230+230=690 $円となり、さらに安くなる。 倹約家の胡桃さんは、このような切符分割をうまく使うことで、交通費を節約しようと考えた。 胡桃さんは、駅$ S $から駅$ G $へ行きたいが、もし可能であれば、切符分割により運賃を安く済ませたい。 しかしながら、切符を何枚も買うのは、胡桃さんにとって面倒である。 そこで胡桃さんは、**最大**$ 2 $枚の切符を使って、駅$ S $から駅$ G $へ移動しようと考えた。 したがって、上記の例において、胡桃さんが駅$ 0 $から駅$ 6 $まで移動する場合には、$ 710 $円が必要となる。 あなたの仕事は、胡桃さんが駅$ S $から駅$ G $へ移動するために必要な交通費の最小値を求めることである。 入力は以下の形式で与えられる。 > $ N $ $ M $ $ K $ $ S $ $ G $ $ a_0 $ $ b_0 $ $ d_0 $ $ a_1 $ $ b_1 $ $ d_1 $ : $ a_{M-1} $ $ b_{M-1} $ $ d_{M-1} $ $ x_0 $ $ f_0 $ $ x_1 $ $ f_1 $ : $ x_{K-1} $ $ f_{K-1} $ - $ 1 $行目には、駅の数$ N $、路線の数$ M $、運賃表のサイズ$ K $が与えられる。 - $ 2 $行目には、出発駅の番号$ S $、到着駅の番号$ G $が与えられる。 - $ 3 $行目から$ M+2 $行目には、路線の情報が与えられる。各行は、駅$ a_i $と$ b_i $を結ぶ、距離$ d_i $の路線が存在することを表す。 - $ M+3 $行目から$ M+K+2 $行目には、運賃表の情報が与えられる。任意の$ j\ (0≦j＜K) $および距離$ l\ (l≧1) $について、$ x_j≦l＜x_{j+1} $を満たすならば、距離$ l $に対する運賃が$ f_j $であることを表す。ただし、$ x_K $は無限大であると仮定する。 入力中の各変数はすべて整数である。また、以下の制約を満たす。 - $ 2≦N≦30000 $ - $ 1≦M≦60000 $ - $ 1≦K≦100 $ - $ 0≦S＜N $ - $ 0≦G＜N $ - $ S≠G $ - 任意の$ 0≦i＜M $に対し、$ 0≦a_i＜N,\ 0≦b_i＜N,\ a_i≠b_i $ - 任意の$ 0≦i＜j＜M $に対し、$ \{a_i,b_i\}≠\{a_j,b_j\} $ - 任意の$ 0≦i＜M $に対し、$ 1≦d_i≦10^4 $ - $ 1=x_0＜x_1＜...＜x_{K-1}≦10^9 $ - $ 1≦f_0＜f_1＜...＜f_{K-1}≦10^9 $ - 駅$ S $から駅$ G $への経路が存在する 切符を最大$ 2 $枚購入するときの、駅$ S $から駅$ G $への運賃の合計の最小値を、$ 1 $行に出力せよ。出力の末尾には改行を入れなければならない。 以下の$ 3 $つの制約を満たすテストケースに正答すると、$ 20 $点を得ることができる。 - $ 2≦N≦100 $ - $ 1≦M≦200 $ - 切符分割により交通費が安くなることはない。 すなわち、駅$ S $から駅$ G $までの切符$ 1 $枚のみを購入するのが最適となる。 以下の$ 2 $つの制約を満たすテストケースに正答すると、$ 20 $点を得ることができる。 - $ 2≦N≦100 $ - $ 1≦M≦200 $ ```

7 6 6
0 6
0 1 6
1 2 7
2 3 6
3 4 8
4 5 5
5 6 9
1 180
7 230
16 400
26 530
41 740
61 820
```

 ```
710
```

- 問題文中に示した通りである。
 
```
7 6 6
4 1
0 1 6
1 2 7
2 3 6
3 4 8
4 5 5
5 6 9
1 180
7 230
16 400
26 530
41 740
61 820
```

 ```
400
```

- 入力例1と路線および運賃表は同じであるが、出発駅および到着駅が異なる。この場合は、駅$ 4 $から$ 1 $までの切符をそのまま買ったほうが良い。
 
```
5 5 4
0 4
0 1 2
1 2 3
2 4 5
1 3 8
3 4 6
1 100
4 200
9 400
16 600
```

 ```
300
```

- ある駅から別の駅への経路は、複数存在することもある。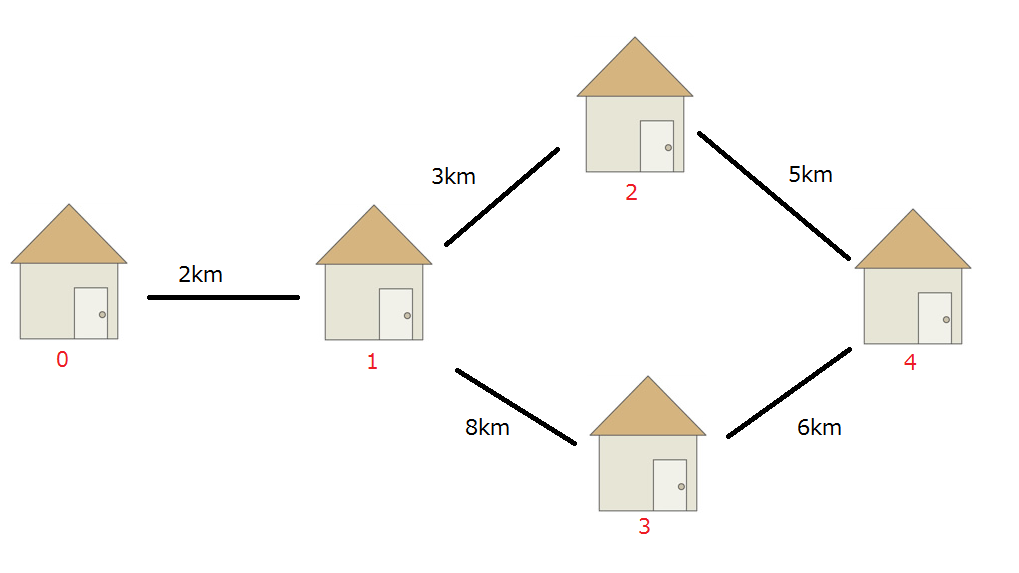

 ![](https://cdn.luogu.com.cn/upload/vjudge_pic/AT_qupc2014_d/c35b108f677d240b355b0d5f50161462c110834f.png)

 ```
2 1 2
0 1
0 1 3
1 100
3 210
```

 ```
210
```
                            

N/A

N/A