AT_qupc2014_g 立ち入り禁止区域

你是一名警察，负责的地区被划分为几种类型的区块，所有区块都是长方形且与坐标轴平行。某天，收到了一起恐怖袭击的预告。袭击只针对生活区块。炸弹爆炸的影响范围是圆形的。由于你的同事非常优秀，所有炸弹的安装位置和爆炸威力（即爆炸半径）都已知。然而，由于时间紧迫，无法拆除炸弹。为了让市民撤离，需要设定一个禁止进入区域。禁止进入区域应包含所有与炸弹爆炸范围重叠的生活区块，并且为一个连通区域。由于炸弹威力可能有一定误差，即使炸弹爆炸范围与生活区块仅仅相切，该生活区块也必须包含在禁止进入区域中。你的任务是准备用于显示禁止进入区域的设备。所有炸弹会同时爆炸，设备是一次性的，即使被炸毁也没关系。设备的数量取决于外周的长度，因此希望外周长度尽可能小。请计算当禁止进入区域的外周长度最小时，这个最小外周长度是多少。输入格式如下所示。 > $N$ $M$ $Cx_0$ $Cy_0$ $Cr_0$ …… $Cx_{N-1}$ $Cy_{N-1}$ $Cr_{N-1}$ $Bx_0$ $By_0$ $Bw_0$ $Bh_0$ …… $Bx_{M-1}$ $By_{M-1}$ $Bw_{M-1}$ $Bh_{M-1}$ 以城市的左右为 $x$ 轴，上下为 $y$ 轴，上和右为正方向。炸弹数量为 $N$，区块数量为 $M$，每个炸弹的位置为 $(Cx, Cy)$，爆炸半径为 $Cr$。每个生活区块的左下顶点为 $(Bx, By)$，左右长度为 $Bw$，上下长度为 $Bh$。输入中的所有变量均为整数，且满足以下约束条件： - $1 \leq N \leq 100$ - $1 \leq M \leq 100$ - $-10000 \leq Cx_i, Cy_i, Bx_i, By_i \leq 10000$ - $1 \leq Cr_i, Bh_i, Bw_i \leq 1000$ 满足以下约束的情况可获得 80 分： - $N = 1$ - $M = 1$ - $-100 \leq Cx_i, Cy_i, Bx_i, By_i \leq 100$ - $1 \leq Cr_i, Bh_i, Bw_i \leq 100$ 请输出禁止进入区域的外周长度 $l$，保留一行。输出的绝对误差需不超过 $10^{-3}$。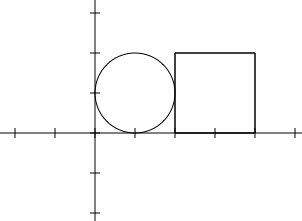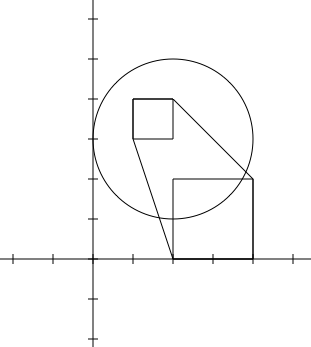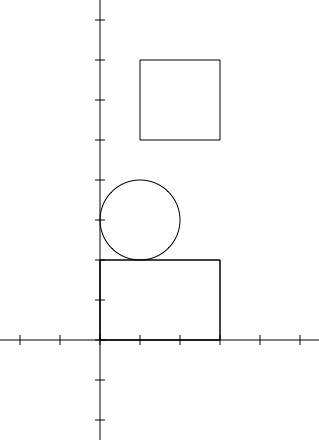 ``` 1 1 1 1 1 2 0 2 2 ``` ``` 8 ```  ``` 1 2 2 3 2 2 0 2 2 1 3 1 1 ``` ``` 11.9907 ```  ``` 1 2 1 3 1 0 0 3 2 1 5 2 2 ``` ``` 10 ``` 

第一行包含两个整数 $N$ 和 $M$，分别表示炸弹的数量和生活区块的数量。 接下来 $N$ 行，每行包含三个整数 $Cx_i$、$Cy_i$、$Cr_i$，表示第 $i$ 个炸弹的位置和爆炸半径。 接下来 $M$ 行，每行包含四个整数 $Bx_i$、$By_i$、$Bw_i$、$Bh_i$，表示第 $i$ 个生活区块的左下顶点坐标、宽度和高度。

输出一行，表示禁止进入区域的最小外周长度 $l$。输出的绝对误差需不超过 $10^{-3}$。

无。 由 ChatGPT 4.1 翻译