AT_qupc2014_g 立ち入り禁止区域
Description
[problemUrl]: https://atcoder.jp/contests/qupc2014/tasks/qupc2014_g
あなたは警官である あなたの担当する地区では、区画がいくつかの種類で分類されており、すべての区画は長方形であり、軸と平行である。 ある日、テロの予告が来た。 テロは生活区画のみを対象としている。 爆弾の爆発の影響のある範囲は円形である。 同僚の警察官は優秀なので、すべての爆弾の設置場所と爆発の威力はわかっている。 しかし、時間が足りないので、爆弾を解除することはできない。 市民を逃がすために立ち入り禁止区域を設定する。 立ち入り禁止区域は爆弾の爆破範囲と重なっている生活区域を含む一つの領域とする。 爆弾の威力は多少ぶれる可能性があるため、爆弾の爆破範囲と生活区域が接している場合も、その生活区域は立ち入り禁止区域に含まれなければならない。 あなたの仕事は、立ち入り禁止区域を表示するための機材を用意することである。 爆弾は全て同時に爆発することがわかっており、立ち入り禁止区域を表示する機材は使い捨てのため、機材が爆発に巻き込まれて壊れてしまっても、問題ない。 機材は外周の長さによって使う数がきまっているため、外周の長さを最小にしたい。 立ち入り禁止区域の外周の長さが最小になる時の、外周の長さを求めよ。 入力は以下の形式で与えられる。
> $ N $ $ M $ $ Cx_0 $ $ Cy_0 $ $ Cr_0 $ ・ ・ $ Cx_{N-1} $ $ Cy_{N-1} $ $ Cr_{N-1} $ $ Bx_0 $ $ By_0 $ $ Bw_0 $ $ Bh_0 $ ・ ・ $ Bx_{M-1} $ $ By_{M-1} $ $ Bw_{M-1} $ $ Bh_{M-1} $
街について、左右をx軸、上下をy軸として、上と右を正の方向として表記する。 爆弾の数N、 区画の数 M、 爆弾の位置( Cx,Cy)、と爆破半径Cr また、各生活区画について、左下の頂点(Bx, By)と、左右の長さBw、上下の長さBhがあたえられる。 入力中は各変数はすべて整数である。また、以下の制約を満たす。 - $ 1≦N≦100 $
- $ 1≦M≦100 $
- $ -10000≦Cx_i,Cy_i,Bx_i,By_i≦10000 $
- $ 1≦Cr_i,Bh_i,Bw_i≦1000 $
以下の制約を満たすケースに正答すると、80点を得ることができる。 - $ N=1 $
- $ M=1 $
- $ -100≦Cx_i,Cy_i,Bx_i,By_i≦100 $
- $ 1≦Cr_i,Bh_i,Bw_i≦100 $
立ち入り禁止区域の外周の長さ$ l $を一行で出力してください 出力の絶対誤差は$ 10^{-3} $以下にしてください。 ```
1 1 1 1 1 2 0 2 2 ``` ```8 ``` 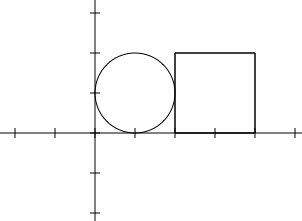 ```1 2 2 3 2 2 0 2 2 1 3 1 1 ``` ```11.9907 ``` 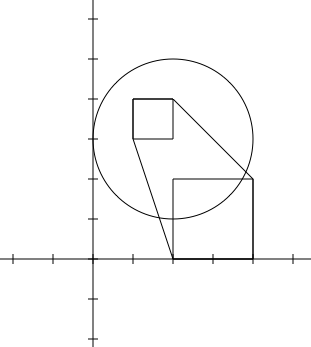 ```1 2 1 3 1 0 0 3 2 1 5 2 2 ``` ```10 ``` 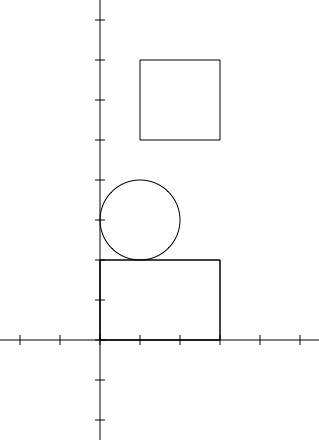
Input Format
N/A
Output Format
N/A