AT_rco_contest_2018_final_b くるくる寿司

[problemUrl]: https://atcoder.jp/contests/rco-contest-2018-final/tasks/rco_contest_2018_final_b この問題はインタラクティブです。$ N $が与えられるので、長さ$ N $の文字列$ S $と、実数$ D $を決めてください。ジャッジは$ S,\ D $から$ Q $個のクエリ$ q_i $を生成します。 $ i $番目のクエリに対し、ジャッジが$ start_i $を、0以上N未満の整数から一様乱数にしたがって選びます。このとき文字列$ q_i $は以下の擬似コードにより決定されます。 > $ q_i\ =\ "" $ for (pos = $ start_i $; $ q_i $.length < M; pos++) 確率 $ 1.0\ /\ D $ で、$ q_i $ の末尾に $ S[pos\ \%\ N] $ を付け足す return $ q_i $ 各$ i $について$ start_i $を推定してください。 各テストケースの得点および、この問題の得点は、次のように計算されます。 - 各$ i $について、$ start_i $の推定値を$ guess_i $としたとき、スコア$ score_i $は以下の数式により計算されます。 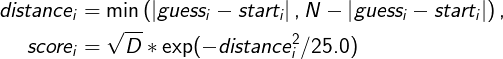 - $ y=exp(-x^2/25) $は以下のようなグラフになります。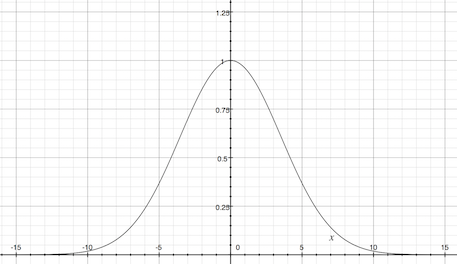  - 1個のテストケースの得点は、各$ i $のスコアの合計を小数点以下切り上げした値になります。 - テストケースは全部で10個あります。各テストケースの得点の合計が、この問題の得点になります。 - なお、スコアの計算に用いられる変数は64ビットの浮動小数点数表現なので、微小な誤差が発生することをご理解ください。 ### Input & Output Format 入力は以下の形式で標準入力から与えられます。 初めに、以下のような入力が与えられます。 > $ N $ $ M $ $ Q $ - $ N $ は$ S $の文字数を表す整数で、$ N\ =\ 3000 $ を満たします。 - $ M $ は$ q_i $の文字数を表す整数で、$ M\ =\ 7 $ を満たします。 - $ Q $ はクエリの個数を表す整数で、$ Q\ =\ 30000 $ を満たします。 この入力に対し、$ S $と$ D $を以下の形式で出力してください。 > $ S $ $ D $ - $ S $は長さ$ N $の文字列で、半角英小文字からなります。 - $ D $は$ 1.0 $以上$ 10.0 $以下の実数です。 その後、以下のような入力が与えられます。 > $ q_0 $ $ q_1 $ ： $ q_{Q-1} $ - $ q_i $ は、$ M $文字の文字列です。 各$ q_i $に対し、$ guess_i $を以下の形式で出力してください。 > $ guess_0 $ $ guess_1 $ ： $ guess_{Q-1} $ - $ guess_i $ は、$ 0\

N/A

N/A

### 背景 Xはある回転寿司屋で一人で寿司を握っています。 今日はXの知人$ Q $人が、回転寿司屋に訪れて食事をします。Xは知人の顔を知らず、さらに客が見えない場所にいますが、知人はSNSに自分の食べる寿司の写真を逐一アップロードするので、Xはそれを見ることで、知人の座っている席をだいたい特定したいと考えました。知人は$ M $回写真をアップロードします。 Xは、特定したい知人に関係無く、決まった長さ$ N $の寿司の列を流し続けます。$ i $番目の知人が着席した瞬間、その目の前には寿司列の$ start_i $番目の寿司が来るとします(この寿司を知人が取るとは限りません)。 また、Xはすでにいる他の客を何人か追い出すことで、それぞれの寿司が知人によって取られる確率を操作することができます。 もちろん客を追い出すと店の評判が落ちるので、寿司列をうまく決め、できるだけ評判が落ちないように知人の位置を特定してください。 ### 入出力例 プログラムへの入力 プログラムの出力 説明 ``` 13 7 2 ``` $ N=13,\ M=7,\ Q=2 $が与えられます。この値はテストケースの制約を満たさないことに注意してください。 ``` nosushinolife 1.8 ``` $ S= $`nosushinolife`$ ,\ D=1.8 $を出力します。$ S $の文字数は$ N=13 $です。 ``` osushin nolifos ``` $ q_0,\ q_1 $が生成され、与えられます。長さはそれぞれ$ M=7 $です。 ``` 1 7 ``` $ guess_0,\ guess_1 $ を出力します。これらは$ 0 $以上$ N $未満でなければなりません。 $ start_0=1,\ start_1=0 $であった場合、スコアは、 $ distance_0\ =\ min(abs(1-1),\ N\ -\ abs(1-1))\ =\ 0, $ $ score_0\ =\ sqrt(D)\ *\ exp(-0^2/25.0) $≒$ 1.341641, $ $ distance_1\ =\ min(abs(7-0),\ N\ -\ abs(7-0))\ =\ 6, $ $ score_1\ =\ sqrt(D)\ *\ exp(-6^2/25.0) $≒$ 0.317872 $ のように計算され、このケースの得点は、 $ score_0\ +\ score_1 $≒$ 1.659513 $を小数点以下切り上げして$ 2 $点となります。 ### テスター テスターを次のリンクから提供しています。 [テスター](https://github.com/recruit-communications/rco-contest-2018/tree/master/final_B/tester)