AT_relay2_b Evergrowing Tree

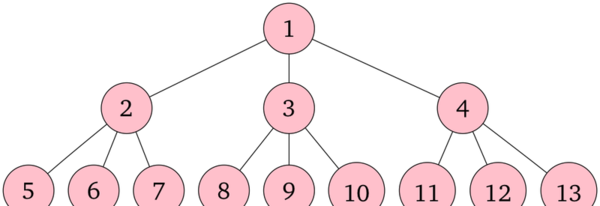[problemUrl]: https://atcoder.jp/contests/cf17-relay-open/tasks/relay2_b 整数 $ N $ が与えられます。下図のような、無限に伸びる完全 $ N $ 分木を考えます。 図: $ N\ =\ 3 $ の場合の無限に伸びる完全 $ N $ 分木 図で示されているように、各頂点には重複しない正の整数の番号が付いており、どの正の整数に対してもそれを頂点番号として持つ頂点が存在します。木の根の頂点番号は $ 1 $ です。その他の頂点には、上の段にある頂点ほど小さな番号が付けられています。同じ段にある頂点には、左に位置するほど小さな番号が付けられています。 この木に関して、以下の形式の $ Q $ 個の問いに答えてください。$ i $ 番目の問い $ (1\

入力は以下の形式で標準入力から与えられる。 > $ N $ $ Q $ $ v_1 $ $ w_1 $ $ : $ $ v_Q $ $ w_Q $

$ Q $ 行出力せよ。$ i $ 行目 $ (1\

### 注釈 - 根付き木において、頂点 $ v $ と $ w $ の *最近共通祖先* とは、頂点 $ v $ と $ w $ のいずれの祖先でもある頂点のうち、最も根から遠いもののことです。ここで、頂点の祖先にはその頂点自身も含まれるものとします。例えば、問題文中で図示された木において、頂点 $ 5 $ と $ 7 $ の最近共通祖先は頂点 $ 2 $、頂点 $ 8 $ と $ 11 $ の最近共通祖先は頂点 $ 1 $、頂点 $ 3 $ と $ 9 $ の最近共通祖先は頂点 $ 3 $ です。 ### 制約 - $ 1\