AT_relay2_b Evergrowing Tree

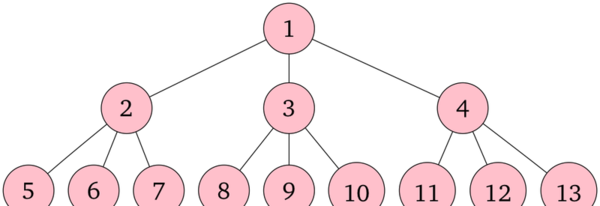
给定一个整数 $N$。请考虑如下图所示的，一个无穷延展的完全 $N$ 叉树。  图：$N = 3$ 的情况下的无穷延展完全 $N$ 叉树 如图所示，每个顶点都被赋予了互不重复的正整数编号，并且对任意正整数，都存在一个编号为该数的顶点。树的根顶点编号为 $1$。其余顶点的编号分配规则为，越靠上的层编号越小，同一层中越靠左编号越小。 现在对于这棵树，你需要回答 $Q$ 个如下格式的询问。第 $i$ 个询问 $(1 \leq i \leq Q)$ 如下： - 求顶点 $v_i$ 和 $w_i$ 的最近公共祖先（参见提示）的顶点编号。

输入通过标准输入给出，格式如下： > $N$ $Q$ $v_1$ $w_1$ $\ldots$ $v_Q$ $w_Q$

输出共 $Q$ 行。第 $i$ 行请输出顶点 $v_i$ 和 $w_i$ 的最近公共祖先的顶点编号。

### 注释 - 对于有根树，两个顶点 $v$ 与 $w$ 的*最近公共祖先*是同时为 $v$ 和 $w$ 祖先的所有顶点中，距离根最远的一个。这里顶点自身也被视为自己的祖先。例如，在题目图示中的树中，顶点 $5$ 和 $7$ 的最近公共祖先为顶点 $2$，顶点 $8$ 和 $11$ 的最近公共祖先为顶点 $1$，顶点 $3$ 和 $9$ 的最近公共祖先为顶点 $3$。 ### 数据范围 - $1 \leq N \leq 10^9$ - $1 \leq Q \leq 10^5$ - $1 \leq v_i < w_i \leq 10^9$ ### 样例解释 1 本例中的询问与注释部分给出的例子相对应。 由 ChatGPT 5 翻译