AT_s8pc_3_e 円と三角形

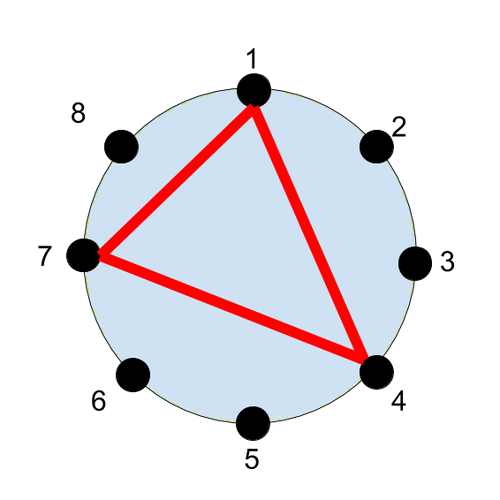
有一个半径为 $1$ 的圆，顶点 $1$ 到 $N$ 按顺时针方向排列在圆周上。 这些顶点将圆周等分为 $N$ 份。 square1001 想从中选出 $3$ 个顶点，构成一个三角形。  在 $\frac{N(N-1)(N-2)}{6}$ 种不同的选法中，请输出按面积从小到大排序后第 $K$ 个三角形的面积。 如果有多个三角形面积相同，只需输出面积即可，顺序无关紧要。 例如，当 $N=4,\ K=3$ 时，情况如下： - 选取顶点编号为 $(1,2,3)$，面积 $=1$ - 选取顶点编号为 $(1,2,4)$，面积 $=1$ - 选取顶点编号为 $(1,3,4)$，面积 $=1$ - 选取顶点编号为 $(2,3,4)$，面积 $=1$ 因此，第 $3$ 个三角形的面积为 $1.0$。 出题者：E869120

输入通过标准输入按以下格式给出。 > $N\ K$ - 第 $1$ 行给出圆周上的点数 $N$ 和表示第几个三角形的整数 $K$，以空格分隔。

- 输出按面积从小到大排序后第 $K$ 个三角形的面积。 - 只要绝对误差或相对误差不超过 $10^{-9}$ 即视为正确。

## 数据范围 - $3 \le N \le 200,\!000$ - $1 \le K \le \frac{N(N-1)(N-2)}{6}$ ## 子任务 子任务1【$160$ 分】 - $N \le 100$ 子任务2【$240$ 分】 - $N \le 1000$ 子任务3【$450$ 分】 - 无额外限制 ## 样例解释 1 本输入样例与题目描述中一致。 ## 样例解释 2 当 $N=6$ 时，面积为 $\frac{\sqrt{3}}{4}$ 的三角形有 $6$ 种选法，面积为 $\frac{\sqrt{3}}{2}$ 的三角形有 $12$ 种选法，面积为 $\frac{3\sqrt{3}}{4}$ 的三角形有 $2$ 种选法。因此，第 $9$ 个三角形的面积为 $\frac{\sqrt{3}}{2}$。 ## 样例解释 3 当 $N=12$ 时，三角形的选法共有 $\frac{12 \times 11 \times 10}{6} = 220$ 种。其中面积最大的是正三角形，因此第 $220$ 个三角形的面积为 $\frac{3\sqrt{3}}{4}$。 由 ChatGPT 4.1 翻译