AT_s8pc_3_h 爆弾ゲーム

[problemUrl]: https://atcoder.jp/contests/s8pc-3/tasks/s8pc_3_h さて, このsquare869120Contest #3も, 最終問題となってしまった。 square1001氏は, 最終兵器として, あるダンジョンに爆弾を仕掛けた。 そのダンジョンは, 左上のマスが $ (0,0) $, 右下のマスが $ (49,49) $ の $ 50\ \times\ 50 $ の大きさである。  その中には, 250個の爆弾が仕掛けられている。位置はすべて違うマスである。 あなたは, 全ての爆弾の位置を知ることで, そのダンジョンから脱出できる。 「そんなん、どうやって知ればいいんだよ！ 全く分かんねぇじゃないか！助けてぇぇぇぇぇ！」 しかし、あなたは以下の質問を何回かできる。 - 左上のマス $ (a,\ b) $, 右下のマス $ (c,\ d) $ の区間に何個爆弾があるかを聞くことができる。 しかし, 質問回数が多くなればなるほど, 爆弾の爆発する確率が高くなり, すなわち生存確率が下がる。 そのため, できるだけ少ない質問回数で爆弾250個の配置を当ててほしい。(その方が得点が高い) あなたの挑戦を待っている。 ### Input & Output Format 最初, 以下のように入力される。 > $ H\ W\ N\ K $ - $ H,\ W $ はダンジョンの大きさである。この問題では, $ H,\ W\ =\ 50 $ である。 - $ N $ はダンジョンの中に含まれる爆弾の数である。この問題では, $ N\ =\ 250 $ である。 - $ K $ は最終的な盤面の状態を出力するために使う整数である。 次に, 次のような質問を何回かすることができる。 質問は以下のような形式で出力することによってできる。 > $ ?\ a\ b\ c\ d $ これは, 左上のマス $ (a,\ b) $, 右下のマス $ (c,\ d) $ の区間に存在する爆弾の数を聞くことである。 また, 質問の返答は, 以下のような出力で行われる。 > $ p $ $ p $ は, 質問で聞いた区間に存在する爆弾の総数である。 また, 答えが分かった時に, 以下のような出力をしなければならない。 > $ !\ ans $ ただし, $ ans $ は以下の値であり, $ r_{i,\ j} $ は, マス $ (i,\ j) $ にある爆弾の個数である。 - $ ans\ =\ \sum_{i=0}^{H-1}\ \sum_{j=0}^{W-1}\ r_{i,\ j}\ 2^{iW\ +\ j} $ mod $ K $

N/A

N/A

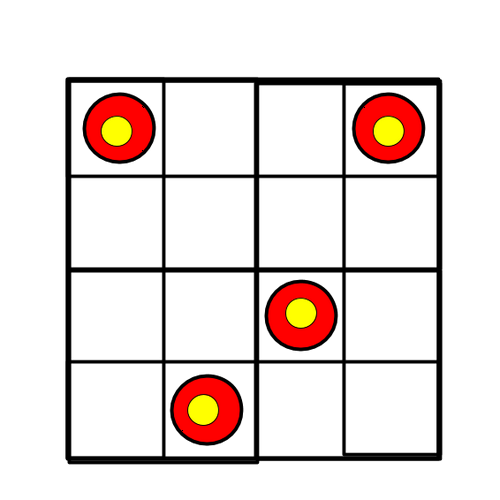
### 制約 - $ H,\ W\ =\ 50 $ - $ N\ =\ 250 $ - $ 1,000,000,000\ \le\ K\ \le\ 1,000,01,000 $ ($ K $はランダムに与えられる) ### 得点 5つのテストケースがある。各テストケースに対する得点は, 以下のように計算される。 - 質問回数を $ Q $ とする。 - $ Q\ >\ 2500 $ のとき, $ 0 $ 点 (Wrong Answer) となる。 - $ 930\ \le\ Q\ \le\ 2500 $ のとき, $ score\ =\ max(\lfloor\ 125\ -\ 3.2\sqrt{Q\ -\ 920}\ \rfloor,\ 40) $ となる。 - $ 880\ \le\ Q $Q ### 入出力例1 例えば, 以下のような配置の場合、以下のような入出力が考えられる。 ただし, この場合 $ H\ =\ W\ =\ 4,\ N\ =\ 4 $ なので, 実際のテストケースには存在しない。 ``` H=4, W=4, N=4 1001 0000 0010 0100 ``` 入出力として考えられる例 プログラムへの入力 プログラムの出力 4 4 4 1000000007 ? 0 0 0 1 1 ? 0 1 0 2 0 ? 0 3 1 3 1 ? 2 1 3 2 2 ? 2 2 2 2 1 ! 9225 ただし, 必ずしも意味のある質問をしているとは限りません。 また, これらの情報で必ずしも盤面が把握できるとは限らず, エスパーをすることも許されはします。