AT_s8pc_4_c Calendar 2

给你一组参数： > $ n $ $ m $ $ q $ $ a_1 $ $ a_2 $ ... $ a_q $ 你需要计算并输出一个整数，代表某种连通部分的数量。 ## 数据范围与说明 ### 约束条件 - $ n \leq 10^{12} $ - $ 7n $ 能够被 $ m $ 整除。 - $ 1 \leq q \leq m \leq 10^5 $ - $ 0 \leq a_1, a_2, \ldots, a_q $ ### 得分详情 - **小任务 1 [100 分]** - $ n \leq 100000 $。 - **小任务 2 [90 分]** - $ m $ 是 $ 7 $ 的倍数。 - 相邻的 $ a_i $ 之间差值为 $ 1 $。 - **小任务 3 [200 分]** - $ m $ 是 $ 7 $ 的倍数。 - **小任务 4 [110 分]** - 无额外约束。 ### 样例说明 1 通过以下形式生成日历，因此，连通部分的数量为 $ 4 $。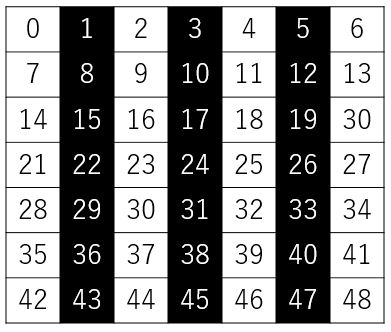  ### 样例说明 2 生成的日历如下所示，连通部分的数量最终被订正为 $ 10 $。  **本翻译由 AI 自动生成**

入力は、次の形式で与えられる。 > $ n $ $ m $ $ q $ $ a_1 $ $ a_2 $ ... $ a_q $

連結な部分の個数を1行に出力しなさい。

### 制約 - $ n $ ≦ $ 10^{12} $ - $ 7n $ は $ m $ で割り切れる。 - 1 ≦ $ q $ ≦ $ m $ ≦ $ 10^5 $ - $ 0 $ ≦ $ a_1 $ a\_2 a\_q ### 得点 小課題1 \[$ 100 $ 点\] - $ n $ ≦ $ 100000 $. 小課題2 \[$ 90 $ 点\] - $ m $ は $ 7 $ の倍数 - $ a_{i\ +\ 1}\ -\ a_i\ =\ 1 $. 小課題3 \[$ 200 $ 点\] - $ m $ は $ 7 $ の倍数 小課題4 \[$ 110 $ 点\] - 追加の制約はない。 ### Sample Explanation 1 次のようなカレンダーになる。よって、連結な部分の個数は $ 4 $ となる。 !\[\](https://atcoder.jp/img/s8pc-4/b7ae283b5c0a566376d05aeff63b100a.png) ### Sample Explanation 2 次のようなカレンダーになる。よって、連結な部分の個数は 14 $ 10 $ (2020/8/08 訂正) となる。 !\[\](https://atcoder.jp/img/s8pc-4/42a03c02d737a1c97005360832707eaa.png)