AT_s8pc_4_d Driving on a Tree
Description
[problemUrl]: https://atcoder.jp/contests/s8pc-4/tasks/s8pc_4_d
配点:$ 800 $ 点
$ N $頂点$ N-1 $辺の連結であるグラフ、つまり、「木」が与えられます。辺 $ i $ は頂点 $ u_i $ と $ v_i $ を結んでいます。
E869120は以下のような操作を行えなくなるまで繰り返します。
- 隣り合った頂点に動く。ただし、同じ頂点を2度通ってはいけない。
- 動ける頂点がない場合、そこで操作は終了となる。
- どこに動くかは等確率にランダムに選ぶ。つまり、次に動ける頂点が$ p $個である場合、それぞれの頂点に$ 1/p $の確率で動くことになる。
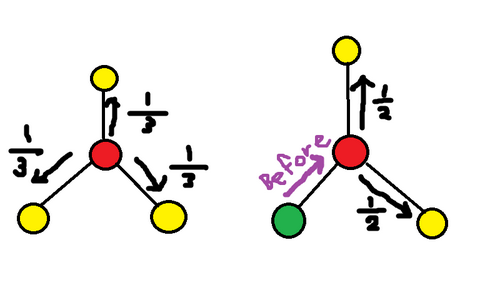
最初、頂点 $ i $ にE869120君がいるとき、動く回数の期待値をすべての $ i $ に対して計算しなさい。
```
5
1 2
2 3
3 4
4 5
```
```
7
1 2
1 3
2 4
2 5
3 6
3 7
```
```
12
1 2
2 3
2 4
4 5
5 6
5 7
6 8
8 9
2 10
10 11
11 12
```
```
2
1 2
```
Input Format
入力は以下の形式で標準入力から与えられる。
> $ N $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ : $ u_{N-1} $ $ v_{N-1} $
Output Format
- $ i $行目に、頂点$ i $から出発した場合の動く回数の期待値を出力しなさい。
- ただし、絶対誤差もしくは相対誤差は$ 10^{-6} $以内でなければなりません。
Explanation/Hint
### 制約
- $ 1\ \le\ N\ \le\ 150,000 $
- 与えられるグラフは連結である。
### 小課題
小課題1 \[ $ 190 $点 \]
- 与えられるグラフは線のようになっている。つまり、どの頂点からも辺が$ 3 $本以上出ていることはない。
小課題2 \[ $ 220 $ 点 \]
- $ 1\ \le\ N\ \le\ 1000 $
小課題3 \[ $ 390 $ 点 \]
- 追加の制約はない。