AT_s8pc_5_i Collecting Gems is Fun

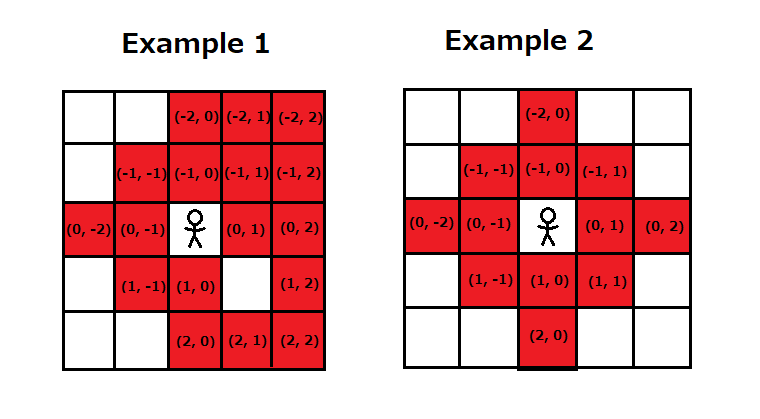
[problemUrl]: https://atcoder.jp/contests/s8pc-5/tasks/s8pc_5_i ある夏の暑い日, E869120 は, AtCoder 公園に行った. 公園は, $ H $ 行 $ W $ 列のグリッドで表される. 左上のマスは $ (1,\ 1) $, 右下のマスは $ (H,\ W) $ である. また, この公園には $ N $ 個の宝石が落ちている. 同じマスに $ 2 $ 個以上の宝石が落ちていることはない. さて, 彼は公園にある宝石を全て集めようと思った. 彼は特別な嗅覚を持っており, 自分で事前に設定した「相対的な位置」に宝石が $ 1 $ つ以上あれば, 「宝石は近い位置にある」という情報が分かる. ただし, 相対的な位置の例は, 以下のようなものである.  上の左から $ 1 $ 番目の図において, E869120 が今マス $ (4,\ 4) $ にいる場合, マス $ (6,\ 5) $ や $ (2,\ 4) $ にある場合は近いと判定される. なぜなら, 自分を $ (0,\ 0) $ として見たときにそれぞれの座標は $ (2,\ 1) $ や $ (-2,\ 0) $ となり, これらは近いから. しかし, マス $ (2,\ 3) $ にある宝石は「近い」と判定されない. なぜなら, 相対的に $ (-2,\ -1) $ は近いマスに含まれないから. さて, 彼は最初マス $ (1,\ 1) $ にいる. 「近い宝石が $ 1 $ 個以上ある」「そうでない」だけの情報で, 全ての宝石をできるだけ短い時間で集める方法を書いたプログラムを書け. ただし, 彼は $ 1 $ マス {左, 右, 下, 上} のどれかの方向に移動するのに $ 1 $ 秒かかり, 自分の今いるマスに宝石がある場合 $ 0 $ 秒で掘ることができると仮定してよい. ### Input & Output Format **この問題はインタラクティブ問題 (プログラムの入力と出力でジャッジとコミュニケーションをとる問題) であり, 入出力の形式が特殊である.** まず, あなたは公園の縦の長さ $ H $, 横の長さ $ W $, 宝石の個数 $ N $ を以下のような形式で受け取る. > $ H $ $ W $ $ N $ 次に, あなたは「近いに含まれる相対的な位置」を設定しなければならない. 以下の形式で設定すること. > $ P $ $ x_1 $ $ y_1 $ $ x_2 $ $ y_2 $ ... $ x_P $ $ y_P $ $ 1 $ 行目に, 近いに含まれる相対的な位置の個数 $ P $ を出力しなければならない. $ 0\ \leq\ P\ \leq\ 500 $ でなければならない. $ 2 $ 行目から $ P $ 行にわたって, 相対的な位置 $ (x_i,\ y_i) $ を出力しなければならない. また, $ x_i,y_i $ の値の絶対値は $ 10^9 $ 以下である必要がある. **ただし, 自分のマスに宝石がある場合すぐに取ってしまうので, $ (x_i,\ y_i)\ \neq\ (0,\ 0) $ でなければならない.** 次に, (☆) -> (★) -> (☆) -> (★) -> ... の順に以下のように処理を繰り返す. (☆) コンピューターがあなたに情報を与える. 情報は以下のような形式で与えられる. > $ S $ 情報は以下のように分類される. - `far`: このマスに宝石はなく, かつあなたが設定した「近い位置」にも宝石はない. - `close`: このマスに宝石はないが, あなたが設定した「近い位置」に宝石はある. - `get-far`: このマスに宝石はあったので E869120 は宝石を取り, その後の状態で「近い位置」に宝石がない. - `get-close`: このマスに宝石はあったので E869120 は宝石を取り, その後の状態で「近い位置」に宝石がある. - `get-clear`: このマスに宝石があったので E869120 は宝石を取り, それで宝石が全て取られたときに必ず出力される. これを受け取ったらすぐにプログラムを終了させること. (★) E869120 が移動する. 以下のような形式で移動の方向を出力すること. > $ c $ $ c $ が `L` のとき左に $ 1 $ マス, `R` のとき右に $ 1 $ マス, `U` のとき上に $ 1 $ マス, `D` のとき下に $ 1 $ マス動くことを意味する. また, 公園の外に出るような移動はしてはならない.

N/A

N/A

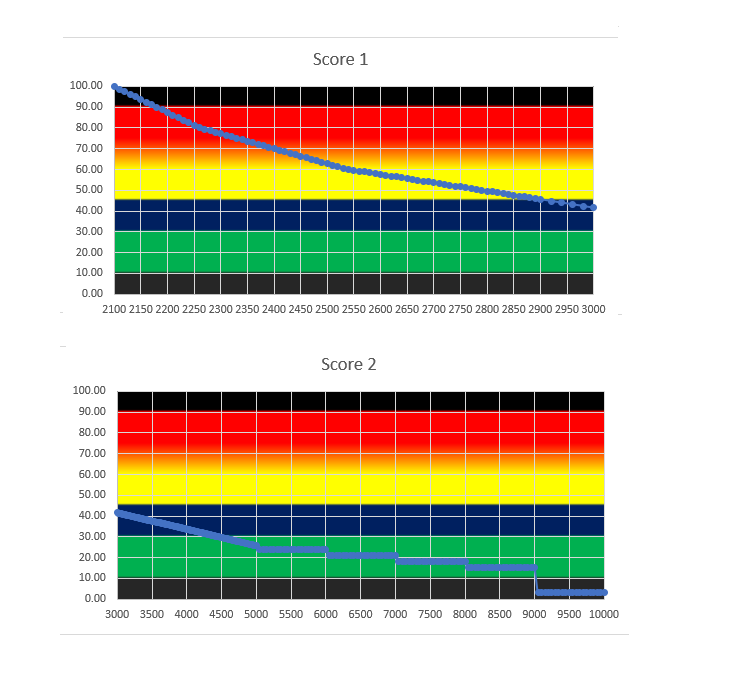
### 注意 出力形式を間違えたり公園の外に出るような移動をした場合の結果は不定である. (WA になるとは限らない) **また, 出力の最後に flush しなければならず, そうしない場合 TLE となることがある.** **E869120 は, $ 10\ 000 $ 回までしか移動をしてはならない.** ### 制約 - $ H\ =\ 100 $ - $ W\ =\ 100 $ - $ N\ =\ 200 $ - **公園の中にある宝石は, $ 10000 $ 個のマスからランダムに $ 200 $ 個選ぶという方法で位置が決められている.** ### 得点 この問題には $ 15 $ 個テストケースがある. $ 1 $ 個あたり $ 100 $ 点で採点される. 移動した回数を $ L $ とおくとき, 各ケースの得点は, 以下のように定まる. - $ L\ \leq\ 2\ 100 $ のとき, $ 100 $ 点. - $ 2\ 101\ \leq\ L\ \leq\ 2\ 260 $ のとき, $ floor(100\ -\ \frac{L\ -\ 2100}{8}) $ 点. - $ 2\ 261\ \leq\ L\ \leq\ 2\ 540 $ のとき, $ floor(80\ -\ \frac{L\ -\ 2260}{14}) $ 点. - $ 2\ 541\ \leq\ L\ \leq\ 3\ 000 $ のとき, $ floor(60\ -\ \frac{L\ -\ 2540}{25}) $ 点. - $ 3\ 001\ \leq\ L\ \leq\ 5\ 000 $ のとき, $ floor(41.6\ -\ \frac{L\ -\ 3000}{125}) $ 点. - $ 5\ 001\ \leq\ L\ \leq\ 6\ 000 $ のとき, $ 24 $ 点. - $ 6\ 001\ \leq\ L\ \leq\ 7\ 000 $ のとき, $ 21 $ 点. - $ 7\ 001\ \leq\ L\ \leq\ 8\ 000 $ のとき, $ 18 $ 点. - $ 8\ 001\ \leq\ L\ \leq\ 9\ 000 $ のとき, $ 15 $ 点. - $ 9\ 001\ \leq\ L\ \leq\ 10\ 000 $ のとき, $ 3 $ 点. 移動回数と得点の関係を表したグラフは, 以下のようになる.  ### 入出力例 以下の図は, この入出力例での公園の状態・「近い位置」の選び方（つまり, ここでは $ 8 $ 近傍）を表している.  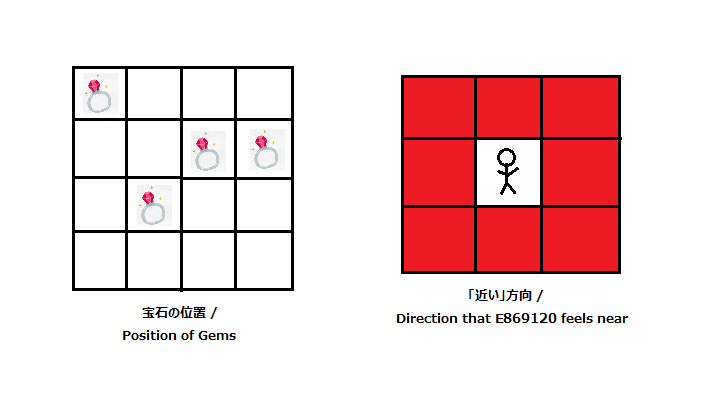例えば, 以下のようなやり取りが行われる. 入力 出力 備考 4 4 4 H, W, N の値を入力. 8 -1 -1 -1 0 -1 1 0 -1 0 1 1 -1 1 0 1 1 「近い位置」に含まれる方向を入力. get-far 今 (1, 1) にいるので, 宝石が取れる. R (1, 2) に動く. close マス (2, 3) にある宝石が「近い」. D (2, 2) に動く. close マス (2, 3), (3, 2) にある宝石が「近い」. D (3, 2) に動く. get-close (3, 2) の宝石を取った. マス (2, 3) にある宝石が「近い」. R (3, 3) に動く. close マス (2, 3), (2, 4) にある宝石が「近い」. U (2, 3) に動く. get-close マス (2, 3) にある宝石を取る. マス (2, 4) にある宝石が「近い」. U (2, 4) に動く. get-clear マス (2, 4) にある宝石を取る. これで全ての宝石が取れた.