AT_s8pc_5_i Collecting Gems is Fun

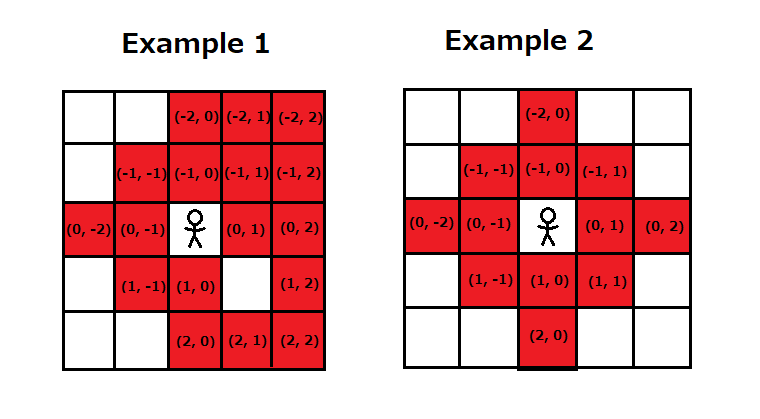
在一个炎热的夏天，E869120 来到了 AtCoder 公园。公园可以被看作一个 $H$ 行 $W$ 列的网格，其中左上角是 $(1, 1)$，右下角是 $(H, W)$。公园里有 $N$ 个宝石，它们分布在不同的格子中，没有两个宝石处于同一个格子。 E869120 决定要收集所有的宝石。他拥有一种独特的能力，能够通过预先设定的一些「相对位置」来感知是否有宝石在「附近」。例如，在下图中，如果他当前位于格子 $(4, 4)$，则可以探测到格子 $(6, 5)$ 和 $(2, 4)$ 的宝石，因为相对坐标是 $(2, 1)$ 和 $(-2, 0)$，这两者被认为是在附近。然而，位于 $(2, 3)$ 的宝石不会被判定为在附近，因为相对位置 $(-2, -1)$ 不在设定的范围之内。  E869120 从格子 $(1, 1)$ 开始移动。请你编写一个程序，利用他所能感知的信息，尽可能高效地收集所有宝石。仅使用「附近有宝石」或「没有宝石」的信息来寻找宝石。E869120 每次只能移动一格，方向可以是左、右、上、下，每次移动用时 $1$ 秒，但拾取当前位置的宝石耗时为 $0$ 秒。 ### 输入格式 这是一个交互式题目，你的程序需要与评测系统实时通信，因此输入输出格式较为不同： 1. 首先，你需要接收公园的尺寸 $H$ 和 $W$，以及宝石的数量 $N$： ``` H W N ``` 2. 接下来，你需设定「附近位置」的相对坐标： ``` P x_1 y_1 x_2 y_2 ... x_P y_P ``` 其中，第一行是「附近位置」的数量 $P$，满足 $0 \leq P \leq 500$。之后的 $P$ 行分别为每个相对位置的坐标 $(x_i, y_i)$，要求 $|x_i|, |y_i| \leq 10^9$，不能为 $(0, 0)$。 然后，在如下步骤中反复进行： 1. 系统给出状态信息： ``` S ``` - `far`: 当前格子和设定的「附近位置」都没有宝石。 - `close`: 当前格子没有，但「附近位置」有宝石。 - `get-far`: 当前格子有宝石，取走后，「附近位置」没有宝石。 - `get-close`: 当前格子有宝石，取走后，「附近位置」仍有宝石。 - `get-clear`: 当前格子上的宝石被取走，并且这是最后一个宝石，此信息出现后程序应立即终止。 2. 你需输出 E869120 的移动方向： ``` c ``` - `L` 表示向左移动一格 - `R` 表示向右移动一格 - `U` 表示向上移动一格 - `D` 表示向下移动一格 注意不可移出网格边界且每次输出后需刷新缓冲区，避免超时。总移动次数不能超过 $10000$ 次。 ### 数据范围与提示 - $ H = 100 $ - $ W = 100 $ - $ N = 200 $ 公园内宝石的位置，是在 $10000$ 个格子中随机选出 $200$ 个位置。 ### 得分规则 每个测试案例满分为 $100$，根据移动次数 $L$ 计算得分： - $ L \leq 2100 $ 时，得 $100$ 分。 - $ 2101 \leq L \leq 2260 $ 时，得分为 $ \lfloor 100 - \frac{L - 2100}{8} \rfloor $。 - $ 2261 \leq L \leq 2540 $ 时，得分为 $ \lfloor 80 - \frac{L - 2260}{14} \rfloor $。 - $ 2541 \leq L \leq 3000 $ 时，得分为 $ \lfloor 60 - \frac{L - 2540}{25} \rfloor $。 - $ 3001 \leq L \leq 5000 $ 时，得分为 $ \lfloor 41.6 - \frac{L - 3000}{125} \rfloor $。 - $ 5001 \leq L \leq 6000 $ 时，得 24 分。 - $ 6001 \leq L \leq 7000 $ 时，得 21 分。 - $ 7001 \leq L \leq 8000 $ 时，得 18 分。 - $ 8001 \leq L \leq 9000 $ 时，得 15 分。 - $ 9001 \leq L \leq 10000 $ 时，得 3 分。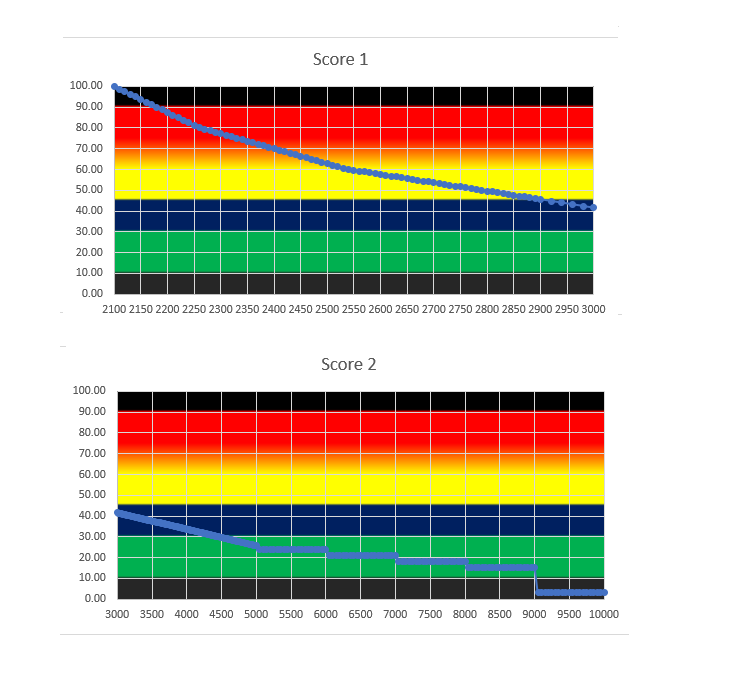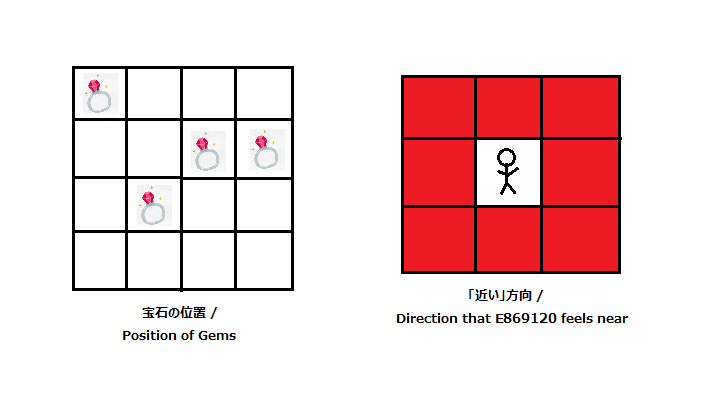 以下是移动次数和得分关系的图示：  ### 示例 下图展示了一个公园的样例状态和选择的「附近位置」（即 8 邻居）的情况：  一个可能的交互示例过程如下： 初始输入为 H, W, N 的值： ``` 4 4 4 ``` 设定「附近位置」： ``` 8 -1 -1 -1 0 -1 1 0 -1 0 1 1 -1 1 0 1 1 ``` 随后的交互过程可能是： ``` get-far R close D close D get-close R close U get-close U get-clear ``` 这表示初始在 $(1, 1)$，通过一系列判断和移动后，E869120 成功收集了所有宝石。 **本翻译由 AI 自动生成**

无

无

### 注意 出力形式を間違えたり公園の外に出るような移動をした場合の結果は不定である. (WA になるとは限らない) **また, 出力の最後に flush しなければならず, そうしない場合 TLE となることがある.** **E869120 は, $ 10\ 000 $ 回までしか移動をしてはならない.** ### 制約 - $ H\ =\ 100 $ - $ W\ =\ 100 $ - $ N\ =\ 200 $ - **公園の中にある宝石は, $ 10000 $ 個のマスからランダムに $ 200 $ 個選ぶという方法で位置が決められている.** ### 得点 この問題には $ 15 $ 個テストケースがある. $ 1 $ 個あたり $ 100 $ 点で採点される. 移動した回数を $ L $ とおくとき, 各ケースの得点は, 以下のように定まる. - $ L\ \leq\ 2\ 100 $ のとき, $ 100 $ 点. - $ 2\ 101\ \leq\ L\ \leq\ 2\ 260 $ のとき, $ floor(100\ -\ \frac{L\ -\ 2100}{8}) $ 点. - $ 2\ 261\ \leq\ L\ \leq\ 2\ 540 $ のとき, $ floor(80\ -\ \frac{L\ -\ 2260}{14}) $ 点. - $ 2\ 541\ \leq\ L\ \leq\ 3\ 000 $ のとき, $ floor(60\ -\ \frac{L\ -\ 2540}{25}) $ 点. - $ 3\ 001\ \leq\ L\ \leq\ 5\ 000 $ のとき, $ floor(41.6\ -\ \frac{L\ -\ 3000}{125}) $ 点. - $ 5\ 001\ \leq\ L\ \leq\ 6\ 000 $ のとき, $ 24 $ 点. - $ 6\ 001\ \leq\ L\ \leq\ 7\ 000 $ のとき, $ 21 $ 点. - $ 7\ 001\ \leq\ L\ \leq\ 8\ 000 $ のとき, $ 18 $ 点. - $ 8\ 001\ \leq\ L\ \leq\ 9\ 000 $ のとき, $ 15 $ 点. - $ 9\ 001\ \leq\ L\ \leq\ 10\ 000 $ のとき, $ 3 $ 点. 移動回数と得点の関係を表したグラフは, 以下のようになる.  ### 入出力例 以下の図は, この入出力例での公園の状態・「近い位置」の選び方（つまり, ここでは $ 8 $ 近傍）を表している.  例えば, 以下のようなやり取りが行われる. 入力 出力 備考 4 4 4 H, W, N の値を入力. 8 -1 -1 -1 0 -1 1 0 -1 0 1 1 -1 1 0 1 1 「近い位置」に含まれる方向を入力. get-far 今 (1, 1) にいるので, 宝石が取れる. R (1, 2) に動く. close マス (2, 3) にある宝石が「近い」. D (2, 2) に動く. close マス (2, 3), (3, 2) にある宝石が「近い」. D (3, 2) に動く. get-close (3, 2) の宝石を取った. マス (2, 3) にある宝石が「近い」. R (3, 3) に動く. close マス (2, 3), (2, 4) にある宝石が「近い」. U (2, 3) に動く. get-close マス (2, 3) にある宝石を取る. マス (2, 4) にある宝石が「近い」. U (2, 4) に動く. get-clear マス (2, 4) にある宝石を取る. これで全ての宝石が取れた.