AT_s8pc_6_c Infinite Grid

[problemUrl]: https://atcoder.jp/contests/s8pc-6/tasks/s8pc_6_c H \* W のマス目があります。上から $ i $ 行目 ($ 1\ \leq\ i\ \leq\ H $)、左から $ j $ 列目 ($ 1\ \leq\ j\ \leq\ W $) にあるマスを、マス $ (i,\ j) $ と呼ぶことにします。 マス $ (i,\ j) $ は、$ c_{i,\ j} $ = `#` のとき黒で塗られており、$ c_{i,\ j} $ = `.` のとき白で塗られています。 下の図は、$ H\ =\ 5,\ W\ =\ 5 $ の場合のマス目の例です。  さて、このマス目を $ 1\ 000\ 000\ 000\ =\ 10^{9} $ 個横に繋げることを考えます。例えば、上の例のマス目を横に $ 10^{9} $ 個繋げると、以下のようになります。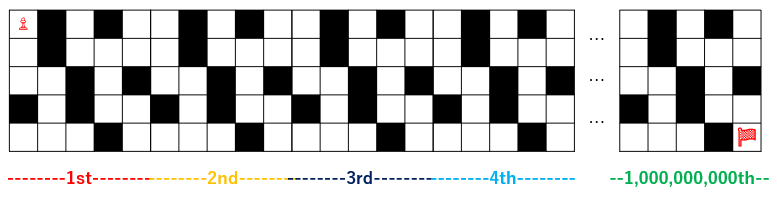  square1001 君は、この広いマス目の中を、左上のマス $ (1,\ 1) $ から右下のマス $ (H,\ 10^9\ \times\ W) $ まで移動します。ただし、以下の条件で移動する必要があります。 - 黒いマスを通らずに移動しなければならない。 - マス $ (i,\ j) $ からは、マス $ (i\ +\ 1,\ j) $ あるいはマス $ (i,\ j\ +\ 1) $ にしか移動することができない。 - マス目の外に出るような移動は許されない。 彼が条件に従って移動できるかどうかを判定してください。

入力は以下の形式で標準入力から与えられます。 > $ H $ $ W $ $ c_{1,\ 1} $$ c_{1,\ 2} $$ c_{1,\ 3} $...$ c_{1,\ W} $ $ c_{2,\ 1} $$ c_{2,\ 2} $$ c_{2,\ 3} $...$ c_{2,\ W} $ $ c_{3,\ 1} $$ c_{3,\ 2} $$ c_{3,\ 3} $...$ c_{3,\ W} $ ... $ c_{H,\ 1} $$ c_{H,\ 2} $$ c_{H,\ 3} $...$ c_{H,\ W} $

square1001 君が左上から右下のマスまで移動できる場合 `Yay!`、移動できない場合 `:(` と出力してください。

### 制約 - $ H,\ W $ は $ 1 $ 以上 $ 100 $ 以下の整数 - $ c_{i,\ j} $ は `#` か `.` のどちらかである - $ c_{1,\ 1} $ は `.` である - $ c_{H,\ W} $ は `.` である ### 部分点 この問題はいくつかの小課題に分けられ、その小課題のすべてのテストケースに正解した場合に「この小課題に正解した」とみなされます。 提出したソースコードの得点は、正解した小課題の点数の合計となります。 1. (60 点) : $ H\ =\ 1 $ 2. (130 点) : $ H\ =\ 2 $ 3. (210 点) : 追加の制約はない。 ### Sample Explanation 1 マス目は次のようになっており、下図のように移動することで目標を達成することができます。 !\[ \](https://img.atcoder.jp/s8pc-6/6029bece14f58346ada477ac29e2f4c2.png) ### Sample Explanation 2 この場合、どうやっても目標を達成できません。それどころか、$ (1,\ 3) $ にすらたどり着くことができません！ !\[ \](https://img.atcoder.jp/s8pc-6/2312a34f846d00092a52dadf81ac90b1.png) ### Sample Explanation 3 下図のように移動すると目標を達成することができます。 !\[ \](https://img.atcoder.jp/s8pc-6/677ff09cf3a28c1bd7accf5b426547ac.png)