AT_s8pc_6_c Infinite Grid

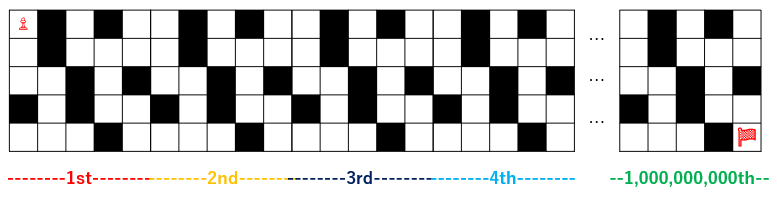
有一个 $H \times W$ 的网格，其中第 $i$ 行（$1 \leq i \leq H$）第 $j$ 列（$1 \leq j \leq W$）的格子称为格子 $(i, j)$。 在格子 $(i, j)$ 中，如果 $c_{i, j} = \texttt{\#}$，则格子是黑色的；如果 $c_{i, j} = \texttt{.}$，则格子是白色的。 下面是一幅 $H = 5, W = 5$ 的网格示例。  接下来，将网格在水平方向上重复 $1\ 000\ 000\ 000 = 10^9$ 次，构建一个超级大网格。例如，以下是上面示例的网格经过 $10^9$ 次水平重复后的示意图。  square1001 君需要从左上角的格子 $(1, 1)$ 出发，到达右下角的格子 $(H, 10^9 \times W)$。但移动过程中需满足以下条件： - 不能通过任何黑色的格子。 - 只能向右（$(i, j) \to (i, j + 1)$）或向下（$(i, j) \to (i + 1, j)$）移动。 - 不允许走出网格的范围。 请判断他是否能按照这些条件从起点成功移动到终点。

输入通过标准输入给出，具体格式为： > $H$ $W$ $c_{1, 1} c_{1, 2} c_{1, 3} \ldots c_{1, W} \ c_{2, 1} c_{2, 2} c_{2, 3} \ldots c_{2, W} \ldots \ c_{H, 1} c_{H, 2} c_{H, 3} \ldots c_{H, W}$

如果 square1001 君能从左上角顺利到达右下角，输出 `Yay!`；否则，输出 `:(`。

- $H, W$ 为 $1$ 至 $100$ 之间的整数。 - $c_{i, j}$ 为 `#` 或 `.`。 - $c_{1, 1}$ 和 $c_{H, W}$ 都是 `.`。 ### 子任务 题目被划分成多个子任务，只有所有测试用例均通过才能完成某个子任务。总得分为所有子任务得分之和。 1. (60 分)：$H = 1$ 2. (130 分)：$H = 2$ 3. (210 分)：无额外限制 ### 样例说明 1 在下面的网格中，可以按照图示路径顺利到达目标位置。  ### 样例说明 2 这种情况下，无论如何都无法到达目标位置，甚至连格子 $(1, 3)$ 也无法抵达。  ### 样例说明 3 可以通过以下路径顺利到达目标。  **本翻译由 AI 自动生成**