AT_s8pc_6_i Garden 2

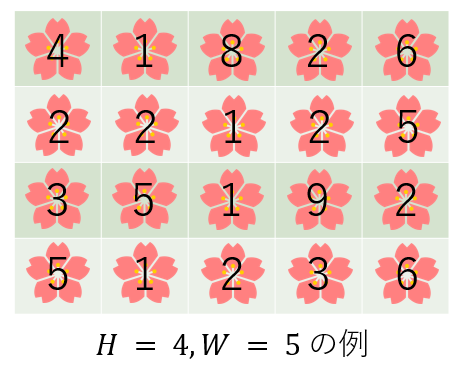
[problemUrl]: https://atcoder.jp/contests/s8pc-6/tasks/s8pc_6_i 時は 2022 年 6 月 20 日。AtCoder は創立 10 周年を記念し、会社の前に庭が作られました。 庭は $ H $ 行 $ W $ 列のマス目で表され、上から $ i $ 行目、左から $ j $ 列目にあるマスを、マス $ (i,\ j) $ とします。 各マスには $ 1 $ つの花が植えられています。マス $ (i,\ j) $ の花の美しさは $ A_{i,\ j} $ です。 例えば、以下のような図が庭の例です。ただし各マスに書かれている数は花の綺麗さです。  さて、あなたはいくつかの花を伐採し、 **美しい庭** を作りたいです。美しい庭とは、以下のような条件を満たすものです。 - 伐採されていない花のマス $ (a,\ b) $ から、別の伐採されていない花のマス $ (c,\ d) $ まで、上下左右に隣り合う伐採されていない花のマスのみを辿って、同じマスを二度通らずに行く方法はちょうど $ 1 $ 通り存在する。 - 全ての伐採されていない花のマス $ (a,\ b) $, $ (c,\ d) $ ($ (a,\ b)\ \neq\ (c,\ d) $) について上が成り立つ。 例えば、以下のような伐採の仕方をすると、美しい庭になります。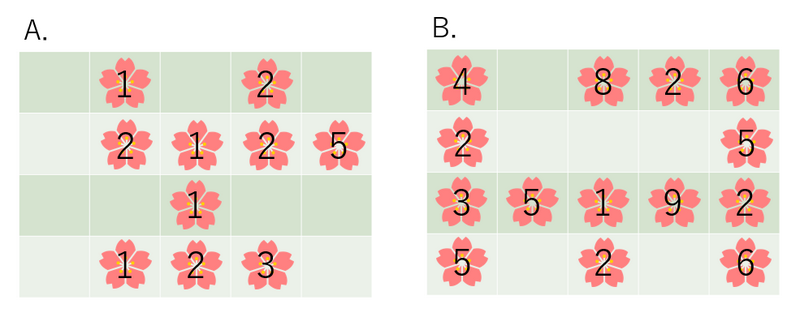  一方、以下のような伐採の仕方をすると、美しい庭にはなりません。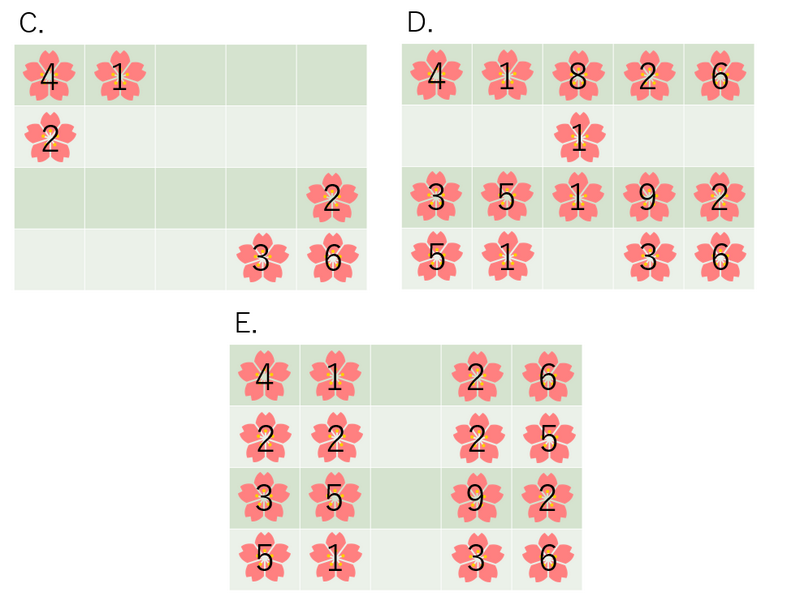  **庭の得点** は、伐採されていない花の綺麗さの合計です。ただし、庭が美しい庭でなければ、庭の得点は $ 0 $ 点となります。 例えば、上の図の庭 $ A $ の得点は $ 20 $ 点、庭 $ B $ の得点は $ 60 $ 点、庭 $ C $, $ D $, $ E $ までの得点は $ 0 $ 点です。 そのとき、庭の得点が出来るだけ高くなるような伐採方法を出力してください。

入力は以下の形式で標準入力から与えられます。 > $ H $ $ W $ $ A_{1,\ 1} $ $ A_{1,\ 2} $ $ A_{1,\ 3} $ ... $ A_{1,\ W} $ $ A_{2,\ 1} $ $ A_{2,\ 2} $ $ A_{2,\ 3} $ ... $ A_{2,\ W} $ $ A_{3,\ 1} $ $ A_{3,\ 2} $ $ A_{3,\ 3} $ ... $ A_{3,\ W} $ ... $ A_{H,\ 1} $ $ A_{H,\ 2} $ $ A_{H,\ 3} $ ... $ A_{H,\ W} $

以下のように $ H $ 行に渡って出力してください。 > $ c_{1,\ 1}c_{1,\ 2}c_{1,\ 3}\ ...\ c_{1,\ W} $ $ c_{2,\ 1}c_{2,\ 2}c_{2,\ 3}\ ...\ c_{2,\ W} $ $ c_{3,\ 1}c_{3,\ 2}c_{3,\ 3}\ ...\ c_{3,\ W} $ ... $ c_{H,\ 1}c_{H,\ 2}c_{H,\ 3}\ ...\ c_{H,\ W} $ ただし、$ c_{i,\ j} $ は、マス $ (i,\ j) $ を伐採 **しない** 場合 `#`、伐採 **する** 場合 `.` としてください。

### 制約 - $ H,\ W $ は $ 1 $ 以上 $ 500 $ 以下の整数 - $ A_{i,\ j} $ は $ 1 $ 以上 $ 9 $ 以下の整数 ### テストケースの生成について テストケースは、以下のように作成されている。 - 各テストケースごとに、$ H,\ W $ の値が決まっている。これに関しては、小課題・得点の項を参照すること。 - $ A_{i,\ j} $ については、各 $ (i,\ j) $ $ (1\ \leq\ i\ \leq\ H,\ 1\ \leq\ j\ \leq\ W) $ について $ 1 $ 以上 $ 9 $ 以下の整数から一様な確率で選ぶ。 ### 小課題・得点 採点に使われるテストケースは $ 15 $ 個存在する。各テストケースごとに $ 100 $ 点満点で採点され、$ 100\ \times\ 15\ =\ 1500 $ 点満点でこの問題の点数が決定する。 各ケースの採点方法は以下のようである。ここでは、そのケースでの「庭の得点」を $ L $ とし、また、$ L'\ =\ L\ \div\ (H\ \times\ W) $ とする。 (☆) $ H\ =\ 5,\ W\ =\ 5 $ (ケース $ 1 $, $ 2 $, $ 3 $) の場合、$ H\ =\ 5,\ W\ =\ 500 $ (ケース $ 4 $, $ 5 $, $ 6 $) の場合の採点方法 - $ 0.00\ \leq\ L'\