AT_s8pc_6_i Garden 2
题目描述
时光回到2022年6月20日。AtCoder为庆祝公司成立十周年,在总部前建造了一个花园。
这个花园能用一个 $H$ 行 $W$ 列的网格表示,每一格的位置用 $(i, j)$ 表示,$i$ 为行号,$j$ 为列号。
每个格子中种着一朵花,花在位置 $(i, j)$ 的美丽度用 $A_{i, j}$ 表示。
例如,下图展示了一个花园,其中每个格子内的数字表示花的美丽度。
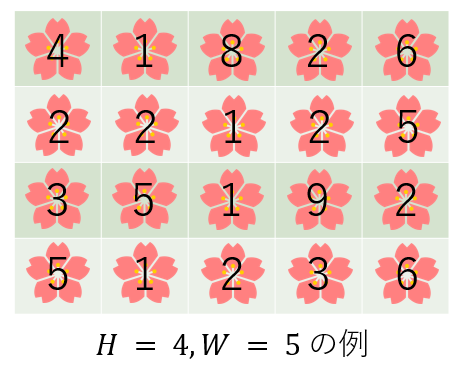
你的任务是砍掉一些花,让花园变得「美丽」。要称为「美丽的花园」,必须满足以下条件:
- 任意两朵未被砍掉的花之间的路径唯一,且路径只能由上下左右相邻的未砍掉的花组成,并且不能经过相同的格子两次。
- 上述条件对于所有未被砍掉的花对 $(a, b)$ 和 $(c, d)$ 均成立(当 $(a, b) \neq (c, d)$)。
例如,以下是一个将花园变得美丽的砍伐方式:
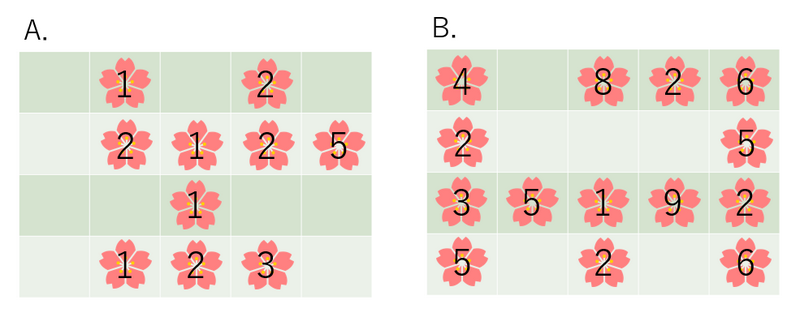
而以下的砍伐方式不能获得「美丽的花园」:
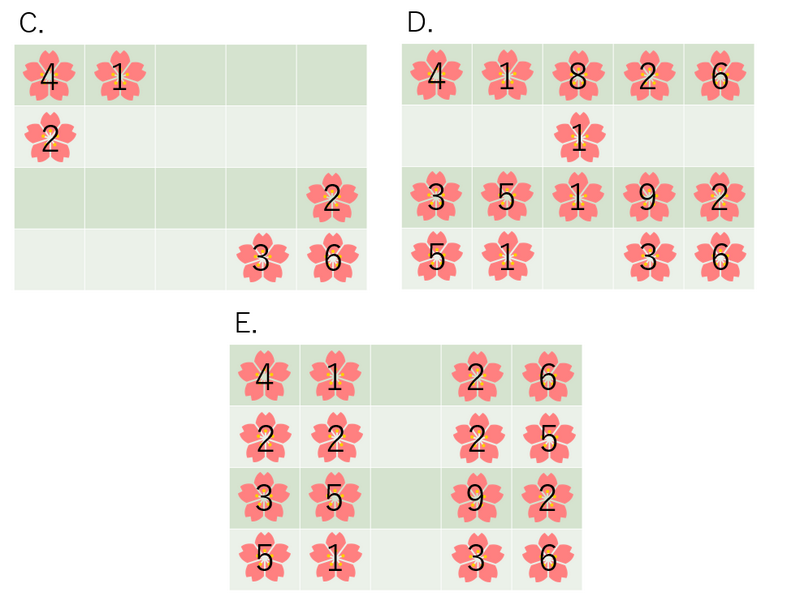
「花园的得分」是所有未被砍掉的花的美丽度之和。如果花园不满足「美丽」条件,得分为 $0$。
例如,上图中的花园 $A$ 得分为 $20$,花园 $B$ 得分为 $60$,而花园 $C$、$D$、$E$ 得分均为 $0$。
请输出一种砍伐方案,使得花园得分尽可能高。
输入格式
输入从标准输入给出,格式如下:
> $H$ $W$ $A_{1, 1}$ $A_{1, 2}$ $A_{1, 3}$ … $A_{1, W}$ $A_{2, 1}$ $A_{2, 2}$ $A_{2, 3}$ … $A_{2, W}$ $A_{3, 1}$ $A_{3, 2}$ $A_{3, 3}$ … $A_{3, W}$ … $A_{H, 1}$ $A_{H, 2}$ $A_{H, 3}$ … $A_{H, W}$
输出格式
请输出 $H$ 行,每行表示花园的一个行:
> $c_{1, 1}c_{1, 2}c_{1, 3}…c_{1, W}$ $c_{2, 1}c_{2, 2}c_{2, 3}…c_{2, W}$ $c_{3, 1}c_{3, 2}c_{3, 3}…c_{3, W}$ … $c_{H, 1}c_{H, 2}c_{H, 3}…c_{H, W}$
其中,如果格子 $(i, j)$ 未被砍掉则用 `#` 表示,砍掉则用 `.` 表示。
说明/提示
### 约束条件
- $H, W$ 均为 $1$ 到 $500$ 之间的整数
- $A_{i, j}$ 为 $1$ 到 $9$ 之间的整数
### 测试数据生成方式
测试用例如下生成:
- 每个测试用例的 $H, W$ 是固定的,具体可见子任务与得分部分。
- $A_{i, j}$ 在 $1$ 至 $9$ 之间随机生成。
### 子任务与得分
总计有 $15$ 个测试用例,每个案例满分 $100$ 分,总分 $1500$ 分。具体计算方法如下。设「花园得分」为 $L$,且 $L' = L \div (H \times W)$。
(☆) 当 $H = 5, W = 5$ (测试用例 $1, 2, 3$)或 $H = 5, W = 500$(测试用例 $4, 5, 6$)时
- $0.00 \leq L' < 2.00$:$0$ 分
- $2.00 \leq L' < 3.33$:$0 + (L - 2.00) \times 21$ 分
- $3.33 \leq L' < 3.93$:$28 + (L - 3.33) \times 40$ 分
- $3.93 \leq L' < 4.03$:$52 + (L - 3.93) \times 480$ 分
- $4.03 \leq L'$:$100$ 分
(★) 当 $H = 500, W = 500$(测试用例 $7$ 到 $15$)时
- $0.00 \leq L' < 2.00$:$0$ 分
- $2.00 \leq L' < 3.33$:$0 + (L - 2.00) \times 21$ 分
- $3.33 \leq L' < 3.78$:$28 + (L - 3.33) \times 75$ 分
- $3.78 \leq L' < 3.84$:$61 + (L - 3.78) \times 650$ 分
- $3.84 \leq L'$:$100$ 分
当 $2.00 \leq L'' \leq 4.05$ 时,得分随 $L'$ 的变化如下图所示:
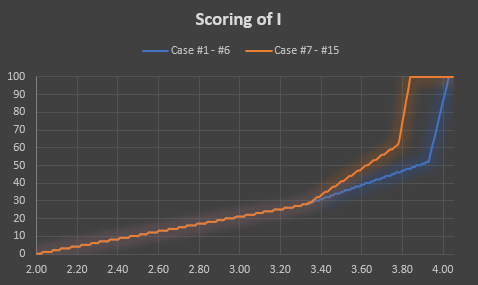
### 注意事项
每当有得分为 $0$ 的测试用例时,将判定为 `WA`。即使得到 `WA`,也有可能获得部分分数;同样,即使得到 `AC`,也不一定满分。
**由于这是一个马拉松类型的题目,不能保证所有测试用例都能得到满分。即使是出题者提供的解法也未必能获得满分。**
**此外,如果发现多数提交超出满分标准,可能会对得分公式进行调整,这种情况的发生概率极小。请注意,比赛开始 3 小时后,得分公式将不会再更改。**
### 样例解释 1
按照示例输出 1 的砍伐方式,花园的得分为 $1 + 3 + 4 + 5 + 6 + 7 + 9 = 35$ 分。请注意,这个例子不在评分数据中。
### 样例解释 2
该输入示例对应于问题描述中的图片,而示例输出 2 对应于例子 B,花园得分为 $60$。此时 $L'$ 的值为 $60 \div 20 = 3.00$。顺便一提,也有使得花园得分达到 $62$ 的方案,但此题并不要求必须输出最大得分。请注意,这个例子也不在评分数据中。
**本翻译由 AI 自动生成**