AT_stpc2025_1_f Decimal Pyramid

`1`, `2`, …, `9` の数字からなる長さ $ N $ の文字列 $ S $ が与えられます。 全部で $ \frac{N(N+1)}{2} $ 個のブロックからなる三角形のピラミッドがあります。 ピラミッドは $ N $ 個の層に分かれており、上から順に層 $ 1, 2, \dots, N $ と番号付けられています。さらに、層 $ i $ $ (1 \le i \le N) $ には $ i $ 個のブロックが左右一列に並んでいます。各ブロックには文字列が書かれており、層 $ i $ の左から $ j $ 番目のブロック $ (1 \le j \le i) $ に書かれている文字列を $ C_{i,j} $ と表します。 $ C_{i,j} $ について、以下のことが成り立ちます。 - $ i = N $ ならば、 $ C_{i, j} $ は $ S $ の $ j $ 番目の文字のみからなる長さ $ 1 $ の文字列である。 - $ 1 \le i < N $ ならば、 $ C_{i, j} $ は $ C_{i+1,j} $ と $ C_{i+1,j+1} $ をこの順に結合したものである。 $ C_{1,1} $ を十進表記の整数として見たときの値を $ 998244353 $ で割ったあまりを求めてください。

入力は以下の形式で与えられる。 > $ N $ $ S $

答えを出力せよ。

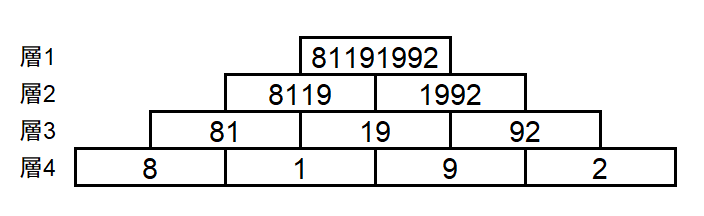
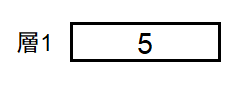
### Sample Explanation 1 $ S = $ `8192` です。ピラミッドは下図の通りになり、 $ C_{1,1} = $ `81191992` です。  ### Sample Explanation 2 $ S = $ `5` です。ピラミッドは下図の通りになり、 $ C_{1,1} = $ `5` です。  ### Constraints - $ N $ は整数 - $ 1 \le N \le 2 \times 10^5 $ - $ S $ は `1`, `2`, …, `9` からなる長さ $ N $ の文字列