AT_stpc2025_1_h Akari Counting

整数 $ H, W, A, B, C, D $ が与えられます。 $ H $ 行 $ W $ 列のマス目があります。上から $ i $ 行目、左から $ j $ 列目のマスをマス $ (i, j) $ と呼びます。 各マスは白または黒で塗られており、マス $ (i, j) $ の色は、 $ A \le i \le B $ かつ $ C \le j \le D $ を満たすとき黒、そうでないとき白です。 このマス目のいくつかの白マスに照明を配置します。白マス $ (i, j) $ に置かれた照明は、以下の $ 2 $ つの条件を満たす白マスすべてを**照らし**ます。 - マス $ (i, j) $ と同じ行または同じ列にある - マス $ (i, j) $ とそのマスの間に黒マスが存在しない 照明の配置は、以下の $ 2 $ つの条件を満たすとき **valid である**と言います。 - すべての白マスが、少なくとも $ 1 $ つの照明に照らされている - 照明のあるマスはいずれも、他の照明によって照らされていない valid な照明の配置の個数を $ 998244353 $ で割ったあまりを求めてください。

入力は以下の形式で与えられる。 > $ H $ $ W $ $ A $ $ B $ $ C $ $ D $

答えを出力せよ。

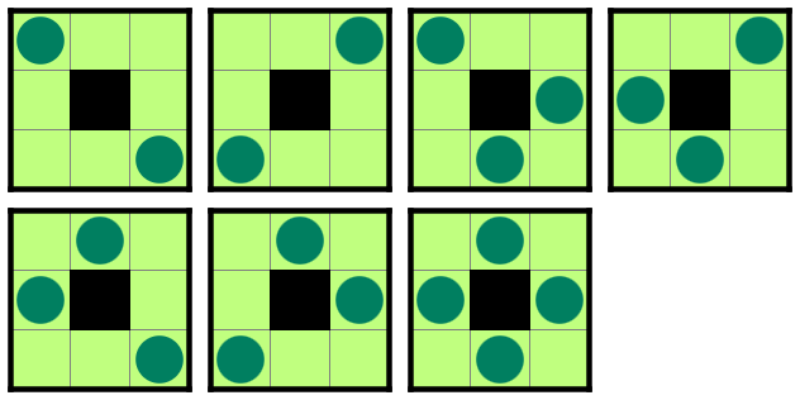
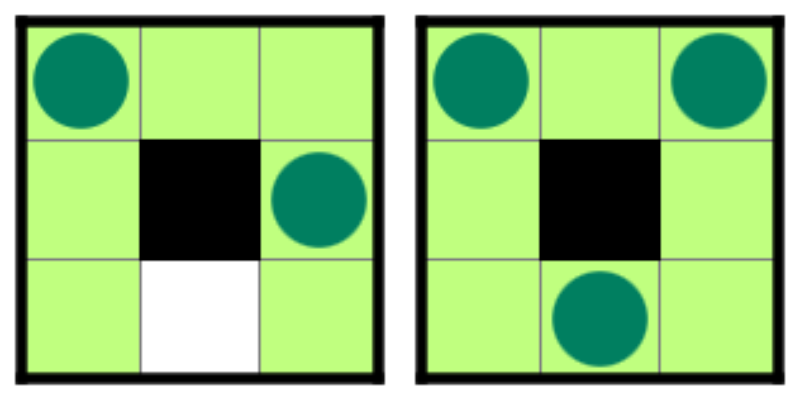### Sample Explanation 1 valid な照明の配置は以下の $ 7 $ 通りです。 ただし、下図では照明及び照明に照らされている白マスは緑色で表しています。  また、以下のような照明の配置は条件を満たしません。 左図の場合、照明に照らされていない白マスがあるため、条件を満たしません。 右図の場合、照明のある白マスであって、他の照明によって照らされているものがあるため、条件を満たしません。 ### Sample Explanation 3 $ 998244353 $ で割ったあまりを出力してください。 ### Constraints - 入力はすべて整数 - $ 1 \leq A \leq B \leq H \leq 5 \times 10^{5} $ - $ 1 \leq C \leq D \leq W \leq 5 \times 10^{5} $ - $ (A, B) \neq (1, H) $ - $ (C, D) \neq (1, W) $