AT_stpc2025_1_i Subgrid Connected Components

$ 2N+1 $ 行 $ 2N+1 $ 列のグリッドが与えられます。ここで、 $ N $ は正整数です。グリッドの上から $ i $ 行目、左から $ j $ 列目のマス $ (1 \le i, j \le 2N + 1) $ をマス $ (i, j) $ と表記します。マス $ (i, j) $ には文字 $ S_{i,j} $ が書かれており、次の性質を満たします。 - $ i $ が奇数、 $ j $ が奇数であるとき、 $ S_{i, j} = $ `o` - $ i $ が奇数、 $ j $ が偶数であるとき、 $ S_{i, j} = $ `-` または `.` - $ i $ が偶数、 $ j $ が奇数であるとき、 $ S_{i, j} = $ `|` または `.` - $ i $ が偶数、 $ j $ が偶数であるとき、 $ S_{i, j} = $ `.` 独立したクエリが $ Q $ 個与えられます。 $ i $ 個目 $ (1 \le i \le N) $ のクエリでは、奇数 $ U_i, D_i, L_i, R_i $ $ (1 \le U_i \le D_i \le 2N+1,\ 1 \le L_i \le R_i \le 2N+1) $ が与えられるので、次の問いに答えてください。 > 部分グリッド $ [U_i, D_i] \times [L_i, R_i] $ において、文字 `o` を頂点、文字 `-` と `|` を辺としたときにできる無向グラフの連結成分の個数を求めてください。 厳密には、次に問いに答えてください。 > $ ((D_i - U_i + 2) / 2) \times ((R_i - L_i + 2) / 2) $ 頂点の無向グラフ $ G $ があり、頂点は $ U_i $ 以上 $ D_i $ 以下の奇数 $ x $ と $ L_i $ 以上 $ R_i $ 以下の奇数 $ y $ のペア $ (x, y) $ で表されるとします。また、無向グラフ $ G $ には次の無向辺があるとし、これら以外の無向辺はないとします。 > > - 奇数 $ x, y $ が $ U_i \le x \le D_i,\ L_i \le y \le R_i - 2 $ かつ $ S_{x,y+1} = $ `-` を満たすならば、頂点 $ (x, y) $ と頂点 $ (x, y+2) $ との間に無向辺がある。 > - 奇数 $ x, y $ が $ U_i \le x \le D_i - 2,\ L_i \le y \le R_i $ かつ $ S_{x+1,y} = $ `|` を満たすならば、頂点 $ (x, y) $ と頂点 $ (x+2, y) $ との間に無向辺がある。 > > 無向グラフ $ G $ の連結成分の個数を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ S_{1,1} $ $ S_{1,2} $ $ \cdots $ $ S_{1,2N+1} $ $ S_{2,1} $ $ S_{2,2} $ $ \cdots $ $ S_{2,2N+1} $ $ \vdots $ $ S_{2N+1,1} $ $ S_{2N+1,2} $ $ \cdots $ $ S_{2N+1,2N+1} $ $ Q $ $ U_1 $ $ D_1 $ $ L_1 $ $ R_1 $ $ U_2 $ $ D_2 $ $ L_2 $ $ R_2 $ $ \vdots $ $ U_Q $ $ D_Q $ $ L_Q $ $ R_Q $

$ Q $ 行出力せよ。 $ i=1,2,\dots, Q $ について $ i $ 行目には $ i $ 番目のクエリに対する答えを出力せよ。

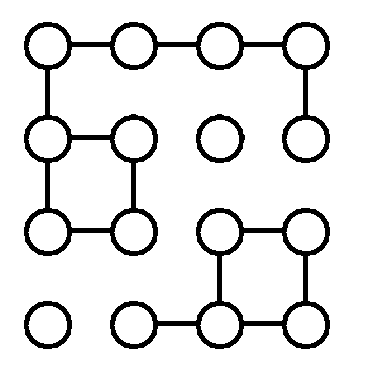
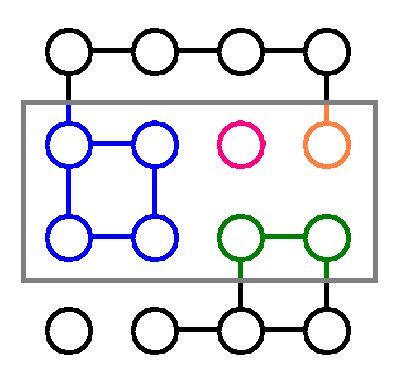
### 注意 この問題のメモリ制限は 384 MiB です。 ### Sample Explanation 1 与えられるグリッドは次のようになっています。  $ 1 $ 番目のクエリにおける答えは、次の図のように $ 4 $ となります。  ### Constraints - $ N $ は整数 - $ 1 \le N \le 2000 $ - $ i $ が奇数、 $ j $ が奇数であるとき、 $ S_{i, j} = $ `o` - $ i $ が奇数、 $ j $ が偶数であるとき、 $ S_{i, j} = $ `-` または `.` - $ i $ が偶数、 $ j $ が奇数であるとき、 $ S_{i, j} = $ `|` または `.` - $ i $ が偶数、 $ j $ が偶数であるとき、 $ S_{i, j} = $ `.` - $ Q $ は整数 - $ 1 \le Q \le 7000 $ - $ 1 \le U_i \le D_i \le 2N+1 $ - $ 1 \le L_i \le R_i \le 2N+1 $ - $ U_i, D_i, L_i, R_i $ は奇数