AT_stpc2025_1_i Subgrid Connected Components
题目描述
给定一个 $2N+1$ 行 $2N+1$ 列的网格,这里 $N$ 是正整数。网格从上到下的第 $i$ 行、从左到右的第 $j$ 列的格子记作 $(i, j)$,满足 $1 \le i, j \le 2N + 1$。在格子 $(i, j)$ 上写有字符 $S_{i,j}$,且满足以下性质:
- 当 $i$ 为奇数且 $j$ 为奇数时,$S_{i, j} = $ `o`
- 当 $i$ 为奇数且 $j$ 为偶数时,$S_{i, j} = $ `-` 或 `.`
- 当 $i$ 为偶数且 $j$ 为奇数时,$S_{i, j} = $ `|` 或 `.`
- 当 $i$ 为偶数且 $j$ 为偶数时,$S_{i, j} = $ `.`
有 $Q$ 个独立的查询。第 $i$ 个查询($1 \le i \le Q$)会给定四个奇数 $U_i, D_i, L_i, R_i$,其中 $1 \le U_i \le D_i \le 2N+1,\ 1 \le L_i \le R_i \le 2N+1$,需要解答下述问题:
> 在子网格 $[U_i, D_i] \times [L_i, R_i]$ 内,以字符 `o` 为顶点、字符 `-` 和 `|` 为边构成的无向图中,连通块(连通分量)的个数是多少?
具体而言,即需要回答下述问题:
> 考虑一个有 $((D_i - U_i + 2) / 2) \times ((R_i - L_i + 2) / 2)$ 个顶点的无向图 $G$,顶点为所有满足 $U_i \le x \le D_i$ 且 $x$ 为奇数,以及 $L_i \le y \le R_i$ 且 $y$ 为奇数的点对 $(x, y)$。此外,无向图 $G$ 仅包含以下无向边:
>
> - 若 $x$、$y$ 为奇数,且 $U_i \le x \le D_i$,$L_i \le y \le R_i - 2$,并且 $S_{x,y+1} = $ `-`,则顶点 $(x, y)$ 和 $(x, y+2)$ 之间连有无向边。
> - 若 $x$、$y$ 为奇数,且 $U_i \le x \le D_i - 2$,$L_i \le y \le R_i$,并且 $S_{x+1,y} = $ `|`,则顶点 $(x, y)$ 和 $(x+2, y)$ 之间连有无向边。
>
> 试求该无向图 $G$ 的连通块数量。
输入格式
输入按照以下格式从标准输入读入:
> $N$
> $S_{1,1}$ $S_{1,2}$ $\cdots$ $S_{1,2N+1}$
> $S_{2,1}$ $S_{2,2}$ $\cdots$ $S_{2,2N+1}$
> $\vdots$
> $S_{2N+1,1}$ $S_{2N+1,2}$ $\cdots$ $S_{2N+1,2N+1}$
> $Q$
> $U_1$ $D_1$ $L_1$ $R_1$
> $U_2$ $D_2$ $L_2$ $R_2$
> $\vdots$
> $U_Q$ $D_Q$ $L_Q$ $R_Q$
输出格式
输出共 $Q$ 行,对于第 $i$ 个查询,在第 $i$ 行输出该查询的答案。
说明/提示
### 注意
本题的内存限制为 384 MiB。
### 样例解释 1
给定的网格如下所示。
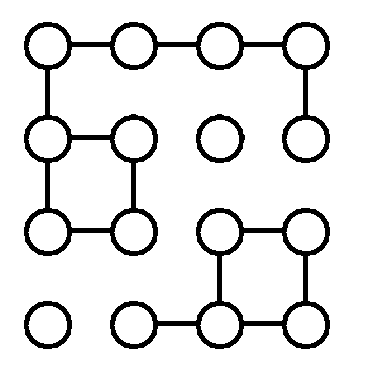
对于第 $1$ 个查询,答案如图所示为 $4$。
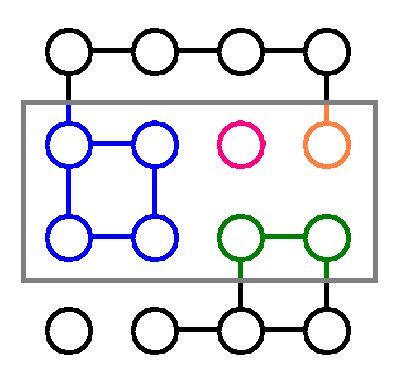
### 数据范围
- $N$ 为整数
- $1 \le N \le 2000$
- 当 $i$、$j$ 为奇数时,$S_{i, j} = $ `o`
- 当 $i$ 为奇数、$j$ 为偶数时,$S_{i, j} = $ `-` 或 `.`
- 当 $i$ 为偶数、$j$ 为奇数时,$S_{i, j} = $ `|` 或 `.`
- 当 $i$、$j$ 为偶数时,$S_{i, j} = $ `.`
- $Q$ 为整数
- $1 \le Q \le 7000$
- $1 \le U_i \le D_i \le 2N+1$
- $1 \le L_i \le R_i \le 2N+1$
- $U_i, D_i, L_i, R_i$ 均为奇数。
由 ChatGPT 5 翻译