AT_stpc2025_1_j Divide Polygon

给定一个正整数 $N$ 和一个大小为 $M$ 的整数集合 $S = \lbrace S_{1}, S_{2}, \dots , S_{M} \rbrace$。 对于 $k = 0, 1, \dots , N - 3$，请回答以下问题。 > 在顶点编号为 $1, 2, \dots, N$ 的正 $N$ 边形中，画出 $k$ 条对角线，并且要求这些对角线不会在顶点以外的地方相交。这样将正 $N$ 边形分割为 $k + 1$ 个多边形。设这些被分割的多边形的边数分别为 $e_{1}, e_{2}, \dots, e_{k + 1}$。 > > 若 $k$ 条对角线的绘制方式满足以下条件，则称之为**好的绘制方式**： > > - $e_{1}, e_{2}, \dots ,e_{k + 1}$ 全都包含在集合 $S$ 中。 > > 求满足上述条件的**好的绘制方式**的数量，对 $998244353$ 取模。

输入格式如下： $ N $ $ M $ $ S_{1} $ $ S_{2} $ $ \dots $ $ S_{M} $

输出 $N-2$ 行。对于 $i=1,2,\dots,N-2$，第 $i$ 行输出当 $k=i-1$ 时的答案。

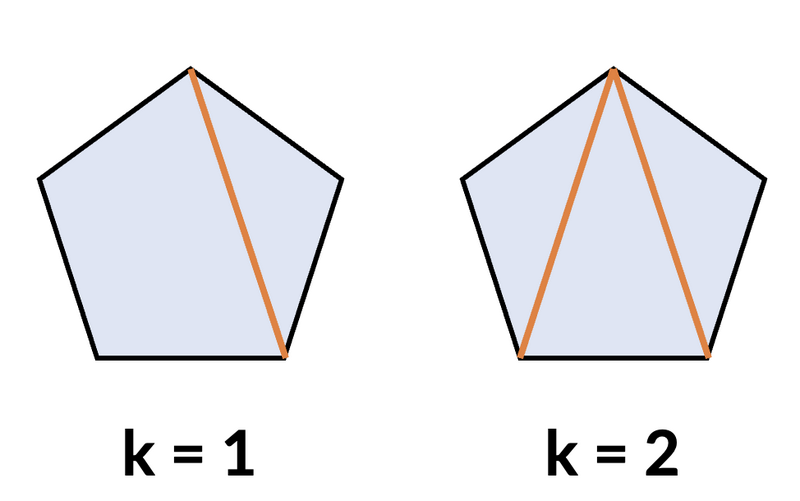
### 样例解释 1 当 $k = 0$ 时，只有 $e_{1} = 5$，但 $5$ 不在 $S$ 中，所以答案为 $0$。 当 $k = 1$ 时，分割出的多边形边数集合必为 $\{3, 4\}$，且两者都在 $S$ 中。正五边形可以画 $1$ 条不相交对角线的方法有 $5$ 种，所以答案为 $5$。 当 $k = 2$ 时，分割出的多边形边数都为 $3$，共有 $3$ 个三角形。正五边形画 $2$ 条互不相交的对角线的方法有 $5$ 种，所以答案为 $5$。  ### 数据范围 - 所有输入都是整数 - $3\leq N\leq 10^{5}$ - $1\leq M\leq N - 2$ - $3\leq S_{i}\leq N$ - $S_{i} < S_{i + 1}$ 由 ChatGPT 5 翻译