AT_stpc2025_1_j Divide Polygon

正整数 $ N $ と、大きさ $ M $ の整数の集合 $ S = \lbrace S_{1}, S_{2}, \dots , S_{M} \rbrace $ が与えられます。 $ k = 0, 1, \dots , N - 3 $ について、以下の問題に答えてください。 > 頂点に $ 1, 2, \dots, N $ の番号が付けられた正 $ N $ 角形に、 $ k $ 本の対角線を頂点以外で互いに交わらないように引きます。 このとき、対角線によって正 $ N $ 角形は $ k + 1 $ 個の多角形に分割されます。これらの分割された多角形の辺の数をそれぞれ $ e_{1}, e_{2}, \dots, e_{k + 1} $ とします。 > > ここで、 $ k $ 本の対角線の引き方が**良い引き方**であるとは、以下の条件を満たすことを言います。 > > - $ e_{1}, e_{2}, \dots ,e_{k + 1} $ がすべて $ S $ に含まれる。 > > $ k $ 本の対角線の**良い引き方**の個数を $ 998244353 $ で割ったあまりを求めてください。

入力は以下の形式で与えられる。 > $ N $ $ M $ $ S_{1} $ $ S_{2} $ $ \dots $ $ S_{M} $

$ N - 2 $ 行出力せよ。 $ i = 1, 2, \dots, N - 2 $ について、 $ i $ 行目には $ k = i - 1 $ のときの答えを出力せよ。

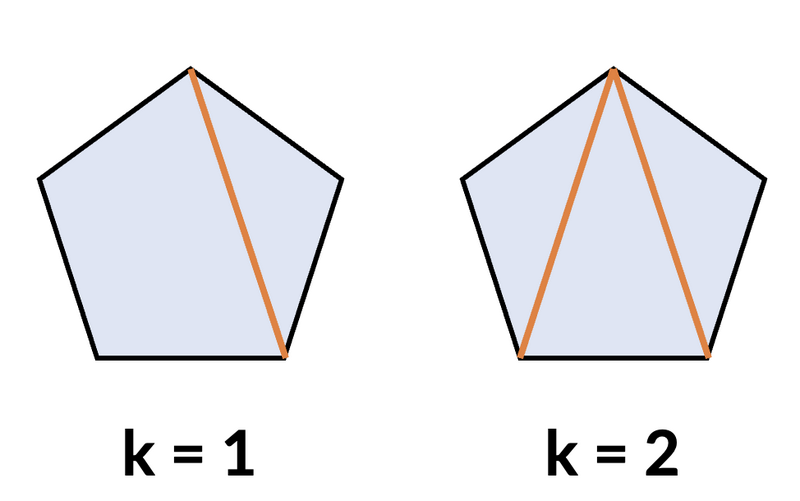
### Sample Explanation 1 $ k = 0 $ のとき、必ず $ e_{1} = 5 $ となります。 $ 5 $ は $ S $ に含まれていないため、答えは $ 0 $ となります。 $ k = 1 $ のとき、必ず $ \{e_{1}, e_{2}\} = \{3, 4\} $ となり、どちらも $ S $ に含まれます。正 $ 5 $ 角形に対角線を $ 1 $ 本引く方法が $ 5 $ 通りあるので、答えは $ 5 $ となります。 $ k = 2 $ のとき、必ず $ e_{i} = 3 \;(1\leq i\leq 3) $ となります。正 $ 5 $ 角形に対角線を互いに交わらないように $ 2 $ 本引く方法が $ 5 $ 通りあるので、答えは $ 5 $ となります。  ### Constraints - 入力はすべて整数 - $ 3\leq N\leq 10^{5} $ - $ 1\leq M\leq N - 2 $ - $ 3\leq S_{i}\leq N $ - $ S_{i} < S_{i + 1} $