AT_stpc2025_2_a Various Roots
题目描述
给定正整数 $N,K$。请判断是否存在一个 $N$ 个顶点的无标号树 $T$,使得以 $T$ 的 $1$ 个顶点作为根节点所能得到的无标号有根树恰好有 $K$ 种。如存在,请输出其中一种。
有 $Q$ 个测试用例,请分别回答每个测试用例。
无标号树指的是**无标号树**,即顶点没有编号、作为图同构的树视为同一个的树。设无标号树 $G,H$ 的顶点集合分别为 $V(G), V(H)$。当且仅当存在一个双射 $\phi: V(G)\to V(H)$,并且满足任意 $u,v \in V(G)$,$uv$ 是 $G$ 的一条边当且仅当 $\phi(u)\phi(v)$ 是 $H$ 的一条边时,$G, H$ 被视为相同的无标号树。
无标号有根树是指:对无标号树 $T$,选取 $T$ 的一个顶点 $r$ 作为**根**,并使其与其他顶点可区分,称为无标号有根树 $(T,r)$。
对于两个无标号有根树 $(G, a), (H, b)$,如果存在一个双射 $\phi: V(G) \to V(H)$,并且满足:
- $\phi(a) = b$。
- 对于任意 $u, v \in V(G)$,$uv$ 是 $G$ 的一条边当且仅当 $\phi(u)\phi(v)$ 是 $H$ 的一条边。
则视为同一个无标号有根树。
输入格式
输入格式如下:
> $Q$ $\text{case}_1$ $\text{case}_2$ $\vdots$ $\text{case}_Q$
其中,$\text{case}_i$ 表示第 $i$ 个测试用例,格式如下:
> $N$ $K$
输出格式
请对每个测试用例按照下述格式输出。若不存在满足条件的无标号树 $T$,输出 `No`。
若存在,任选一种为顶点标号 $1,2,\cdots,N$,按如下格式输出 $T$ 的所有边:
> Yes $u_1$ $v_1$ $u_2$ $v_2$ $\vdots$ $u_{N-1}$ $v_{N-1}$
其中,$u_i \ v_i$ 表示 $T$ 的第 $i$ 条边连接顶点 $u_i$ 与顶点 $v_i$。
说明/提示
## 部分分
对于额外限制 $N \le 5$ 的数据,答对即可获得 $10$ 分。
## 样例解释 1
对于第 $1$ 个测试用例,输出的是 $4$ 个顶点的星形图。
当以黑色节点为根时,上排 $3$ 个无标号有根树按题意被视为同一种。
下排的无标号有根树则与其他 $3$ 个均不同,因此该树能生成 $2$ 种无标号有根树,满足条件。
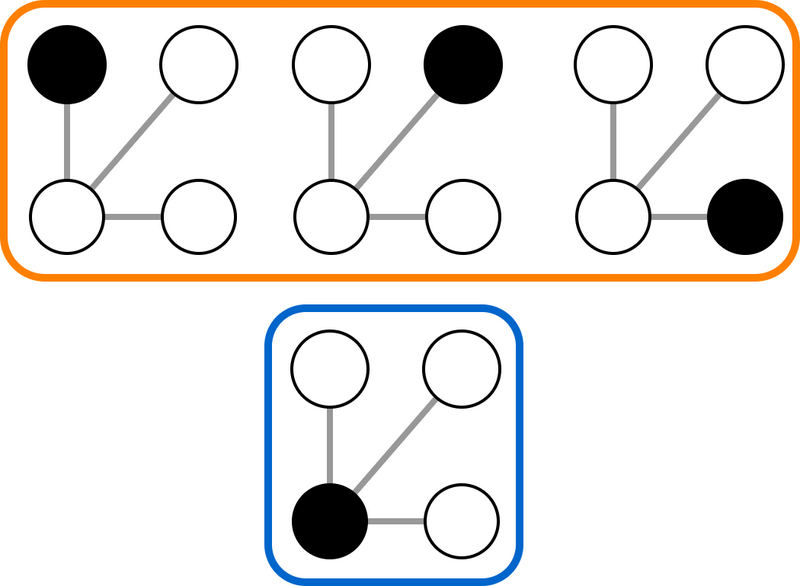
而且,顶点编号可以任意,只需边集为 $\{(3,4), (3,2), (3,1)\}$ 即可,因此这种编号方式也正确。
对于第 $2$ 个测试用例,没有满足条件的无标号树。
该样例满足 $N \le 5$ 的部分分限制。
## 样例解释 2
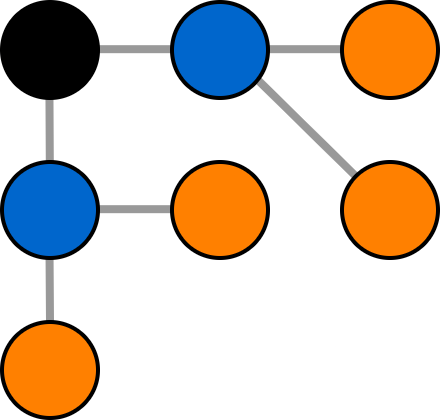
对于第 $1$ 个测试用例,输出的无标号树如下图。
同色的节点作为根时,得到的无标号有根树视为同一种。
因此,本例恰好能得到 $3$ 种无标号有根树,满足条件。
# 数据范围
- 所有输入均为整数。
- $1 \le Q \le 1000$
- $1 \le K \le N \le 1000$
- 所有测试用例中的 $N$ 总和不超过 $2000$。
由 ChatGPT 5 翻译