AT_stpc2025_2_a Various Roots

正整数 $ N,K $ が与えられます。 $ N $ 頂点のラベルなし木 $ T $ であって、 $ T $ の $ 1 $ 頂点を根とすることによって作られるラベルなし根付き木がちょうど $ K $ 通りあるようなものが存在するかどうか判定し、存在するならひとつ出力してください。 $ Q $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。 ラベルなし木とは**ラベルなし木** とは、頂点に区別のための番号が付いておらず、グラフとして同型なものを同一視する木のことです。 ラベルなし木 $ G, H $ の頂点集合をそれぞれ $ V(G), V(H) $ とします。 $ 2 $ つのラベルなし木 $ G, H $ は、以下を満たす全単射 $ \phi : V(G) \to V(H) $ が存在するとき、かつそのときに限り同一視します。 - 任意の $ 2 $ 頂点 $ u, v \in V(G) $ について、辺 $ uv $ が $ G $ に存在することと、辺 $ \phi(u)\phi(v) $ が $ H $ に存在することが同値である。 ラベルなし根付き木とはラベルなし木 $ T $ に対して、 $ T $ のある頂点 $ r $ を **根** として他の頂点から区別できるようにしたものを、**ラベルなし根付き木** $ (T, r) $ と呼びます。 $ 2 $ つのラベルなし根付き木 $ (G, a), (H, b) $ は、以下を満たす全単射 $ \phi : V(G) \to V(H) $ が存在するとき、かつそのときに限り同一視します。 - $ \phi(a) = b $ である。 - 任意の $ 2 $ 頂点 $ u, v \in V(G) $ について、辺 $ uv $ が $ G $ に存在することと、辺 $ \phi(u)\phi(v) $ が $ H $ に存在することが同値である。

入力は以下の形式で与えられる。 > $ Q $ $ \text{case}_1 $ $ \text{case}_2 $ $ \vdots $ $ \text{case}_Q $ ここで、 $ \text{case}_i $ は $ i $ 番目のテストケースを表し、次の形式で与えられる。 > $ N $ $ K $

各テストケースについて、以下の形式で出力せよ。 問題文の条件を満たすラベルなし木 $ T $ が存在しない場合は、`No` と出力せよ。 問題文の条件を満たすラベルなし木 $ T $ が存在する場合は、 $ T $ の頂点に任意の順番で $ 1,2,\cdots,N $ の番号を付け、 $ T $ の辺を以下の形式で出力せよ。 > Yes $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_{N-1} $ $ v_{N-1} $ ここで、 $ u_i\ v_i $ は $ T $ の $ i $ 番目の辺が頂点 $ u_i $ と頂点 $ v_i $ を結ぶことを表す。

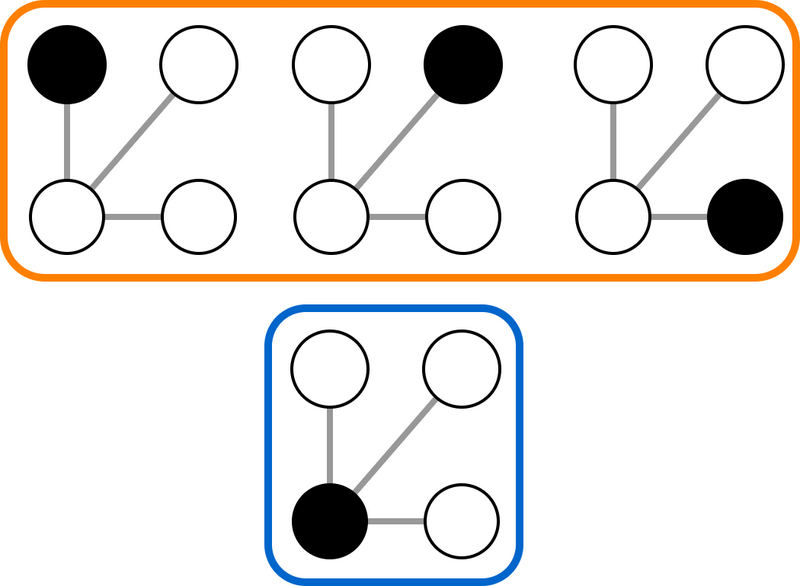
### 部分点 追加の制約 $ N \le 5 $ を満たすデータセットに正解した場合は $ 10 $ 点が与えられる。 ### Sample Explanation 1 $ 1 $ つ目のテストケースでは、 $ 4 $ 頂点のスターグラフが出力されています。 黒色の頂点を根として見た時に、上段の $ 3 $ つのラベルなし根付き木はすべて同一のものとして扱われます。 また、下段のラベルなし根付き木は他 $ 3 $ つのラベルなし根付き木と異なるものとして扱われるため、このラベルなし木によって $ 2 $ 通りのラベルなし根付き木が作られます。よって、このラベルなし木は条件を満たしています。  また、どのような番号の付け方をしても良いため、辺集合が $ \lbrace (3,4),(3,2),(3,1) \rbrace $ となるように番号を付けても正解となります。 $ 2 $ つ目のテストケースでは、条件を満たすラベルなし木は存在しません。 この入力例は、部分点の制約を満たします。 ### Sample Explanation 2 $ 1 $ つ目のテストケースでは、下図のラベルなし木が出力されています。 このラベルなし木では同じ色の頂点からどの頂点を根に選んでも、同一のラベルなし根付き木が作られます。 したがって、 $ 3 $ 通りのラベルなし根付き木が得られ、このラベルなし木は条件を満たしています。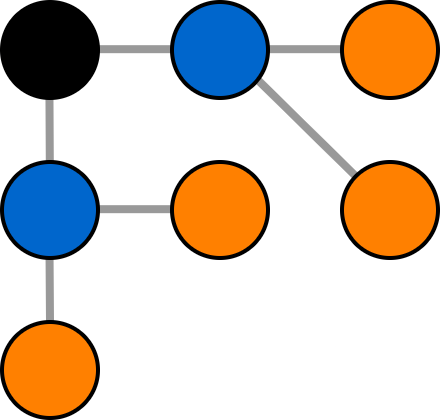  ### Constraints - 入力はすべて整数 - $ 1 \le Q \le 1000 $ - $ 1 \le K \le N \le 1000 $ - $ 1 $ つの入力の中のテストケースすべてにわたる $ N $ の総和は $ 2000 $ 以下