AT_stpc2025_2_d Boomerang
题目描述
给定正整数 $A, B, C, D$。
请判断在二维平面上是否存在互不相同的 $4$ 个点 $p, q, r, s$,满足以下所有条件:
- $p$ 与 $q$ 的欧几里得距离为 $A$。
- $q$ 与 $r$ 的欧几里得距离为 $B$。
- $r$ 与 $s$ 的欧几里得距离为 $C$。
- $s$ 与 $p$ 的欧几里得距离为 $D$。
- 四边形 $pqrs$ 不自交。即,线段 $pq, qr, rs, sp$ 除端点外没有交点。
- 四边形 $pqrs$ 的四个内角中至少有一个大于 $180$ 度。
共给出 $T$ 组测试数据,请分别判断每组数据。
输入格式
输入如下形式:
> $T$ $\mathrm{case}_1$ $\mathrm{case}_2$ $\vdots$ $\mathrm{case}_T$
其中,$\mathrm{case}_i$ 表示第 $i$ 组测试数据,每组测试数据为:
> $A$ $B$ $C$ $D$
输出格式
输出 $T$ 行。
第 $i$ 行($1 \leq i \leq T$),若存在满足题意的 $4$ 个点 $p, q, r, s$,输出 `Yes`,否则输出 `No`。
说明/提示
### 样例解释 1
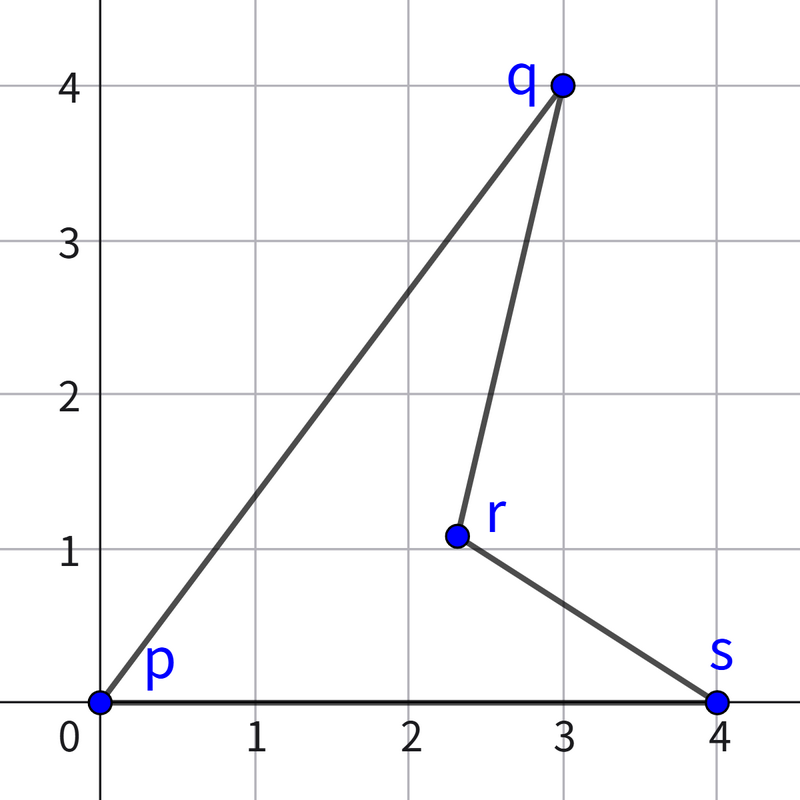
在第 $1$ 组测试数据中,取点 $p$ 为 $(0,0)$,点 $q$ 为 $(3,4)$,点 $r$ 为 $\left(\frac{62}{17} - \frac{16\sqrt{2}}{17}, \frac{24}{17} - \frac{4\sqrt{2}}{17}\right)$,点 $s$ 为 $(4, 0)$ 时,内角 $qrs$ 大于 $180$ 度,且满足所有条件。
### 数据范围
- 所有输入均为整数。
- $1 \leq T \leq 10^5$
- $1 \leq A, B, C, D \leq 10^9$
由 ChatGPT 5 翻译