AT_stpc2025_2_d Boomerang

正整数 $ A,B,C,D $ が与えられます。 $ 2 $ 次元平面上の相異なる $ 4 $ 点 $ p,q,r,s $ であって、次の条件をすべて満たすものが存在するかどうか判定してください。 - $ p $ と $ q $ のユークリッド距離は $ A $ である。 - $ q $ と $ r $ のユークリッド距離は $ B $ である。 - $ r $ と $ s $ のユークリッド距離は $ C $ である。 - $ s $ と $ p $ のユークリッド距離は $ D $ である。 - 四角形 $ pqrs $ は自己交叉しない。すなわち、線分 $ pq,qr,rs,sp $ は端点以外に他の線分と交点を持たない。 - 四角形 $ pqrs $ の内角のうち $ 1 $ つは、 $ 180 $ 度より大きい。 $ T $ 個のテストケースが与えられるので、それぞれについて解いてください。

入力は以下の形式で与えられる。 > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ ここで、 $ \mathrm{case}_i $ は $ i $ 番目のテストケースを表す。各テストケースは以下の形式で与えられる。 > $ A $ $ B $ $ C $ $ D $

$ T $ 行出力せよ。 $ i $ 行目 $ (1\leq i\leq T) $ には、 $ i $ 番目のテストケースについて、問題文の条件を満たす $ 4 $ 点 $ p,q,r,s $ が存在する場合は `Yes` を、そうでないならば `No` を出力せよ。

### Sample Explanation 1 $ 1 $ 番目のテストケースでは、点 $ p $ を $ (0,0) $ 、点 $ q $ を $ (3,4) $ 、点 $ r $ を $ (\frac{62}{17} - \frac{16\sqrt{2}}{17}, \frac{24}{17} - \frac{4\sqrt{2}}{17}) $ 、点 $ s $ を $ (4, 0) $ とすると、内角 $ qrs $ は $ 180 $ 度より大きくなり、すべての条件を満たします。 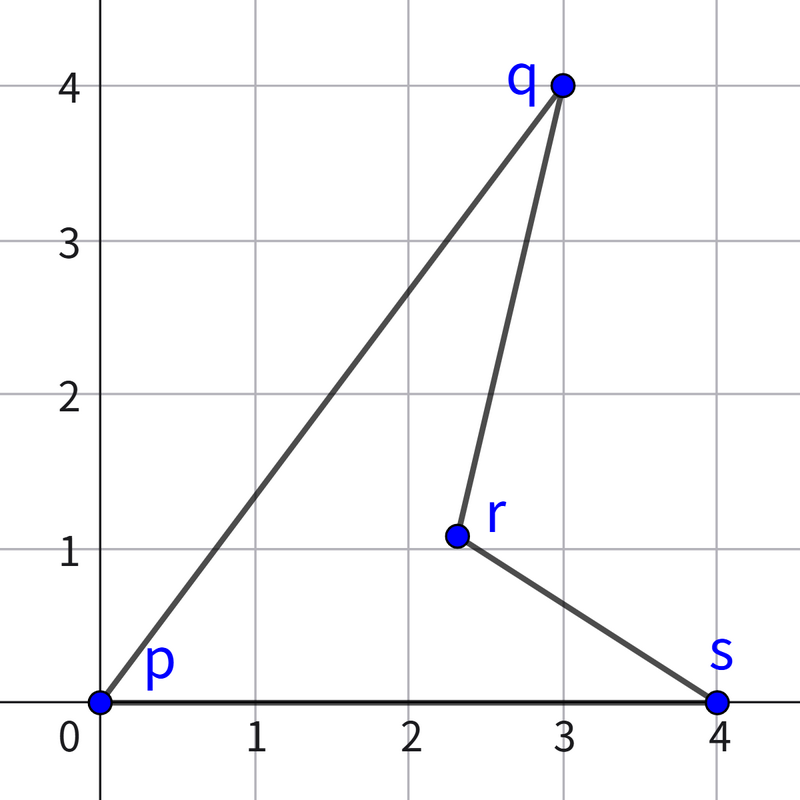 ### Constraints - 入力はすべて整数 - $ 1\le T\le 10^5 $ - $ 1\le A,B,C,D\le 10^9 $