AT_stpc2025_2_j KinGin's Summit

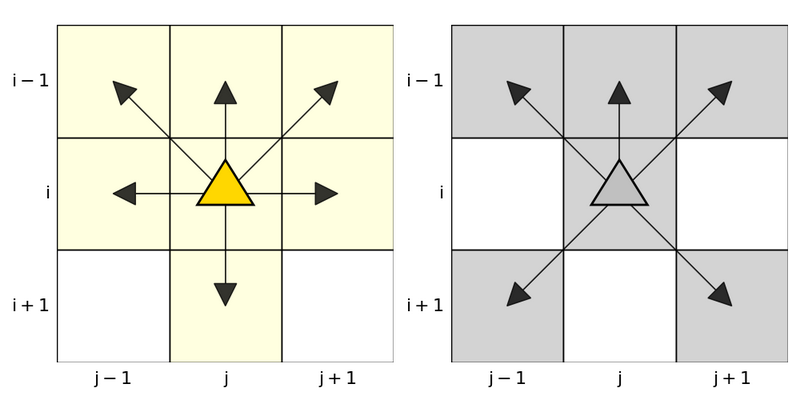
有一个无限大的二维网格。 在网格上有 $N$ 个人，第 $i$ 个人初始位于格点 $(R_i, C_i)$。每个人都戴着金色或银色的帽子。当 $H_i =\texttt{G}$ 时，第 $i$ 个人戴着金色帽子；当 $H_i =\texttt{S}$ 时，戴着银色帽子。 每一回合，每个人会根据帽子的颜色，从当前位置按如下方式移动： - 戴金色帽子的人： 可以原地不动，或者像将棋中的金将一样移动。具体来说，若当前位于 $(i, j)$，则可移动到格点 $(i-1, j-1),\ (i-1, j),\ (i-1, j+1),\ (i, j-1),\ (i, j),\ (i, j+1),\ (i+1, j)$ 中的任一格。 - 戴银色帽子的人： 可以原地不动，或者像将棋中的银将一样移动。具体来说，若当前位于 $(i, j)$，则可移动到格点 $(i-1, j-1),\ (i-1, j),\ (i-1, j+1),\ (i, j),\ (i+1, j-1),\ (i+1, j+1)$ 中的任一格。  请你求出，为了让所有 $N$ 个人汇聚到同一个格点，所需的最小回合数。 有 $T$ 组测试数据，分别输出每组数据的答案。

输入按照以下格式给出。 > $T\ \mathrm{case}_1\ \mathrm{case}_2\ \cdots\ \mathrm{case}_T$ 其中，$\mathrm{case}_i$ 表示第 $i$ 个测试用例，每一组测试如下格式： > $N$ $R_1$ $C_1$ $H_1$ > $R_2$ $C_2$ $H_2$ > $\vdots$ > $R_N$ $C_N$ $H_N$

请对每个测试用例按照顺序输出一行答案。

### 部分分 如果你能解决 $H_i = \texttt{G}$ 的数据集（仅有金帽），可获得 $30$ 分。 ### 样例解释 1 对于第 $1$ 个测试用例，例如可以按如下方式移动，在 $2$ 回合内所有人汇聚到同一格： - 第 $1$ 回合 - 第 $1$ 个人走到 $(2, 2)$ - 第 $2$ 个人走到 $(3, 3)$ - 第 $2$ 回合 - 第 $1$ 个人留在原地 - 第 $2$ 个人走到 $(2, 2)$ 对于第 $2$ 个测试用例，例如可以按如下方式移动，在 $2$ 回合内所有人汇聚到同一格： - 第 $1$ 回合 - 第 $1$ 个人走到 $(1, 2)$ - 第 $2$ 个人走到 $(1, 3)$ - 第 $3$ 个人走到 $(1, 2)$ - 第 $2$ 回合 - 第 $1$ 个人留在原地 - 第 $2$ 个人走到 $(1, 2)$ - 第 $3$ 个人留在原地 对于第 $3$ 个测试用例，所有人一开始就在同一格。 ### 样例解释 2 对于第 $1$ 个测试用例，例如可以按如下方式移动，在 $2$ 回合内所有人汇聚到同一格： - 第 $1$ 回合 - 第 $1$ 个人走到 $(2, 1)$ - 第 $2$ 个人走到 $(2, 2)$ - 第 $2$ 回合 - 第 $1$ 个人留在原地 - 第 $2$ 个人走到 $(2, 1)$ 这个输入样例满足部分分的限制。 ### 约束条件 - $T, N, R_i, C_i$ 为整数 - $1 \le T \le 10^5$ - $1 \le N \le 2 \times 10^5$ - $1 \le R_i \le 10^9$ - $1 \le C_i \le 10^9$ - $H_i$ 为 `G` 或 `S` - 所有测试用例的 $N$ 之和不超过 $2\times 10^5$ 由 ChatGPT 5 翻译