AT_stpc2025_2_j KinGin's Summit

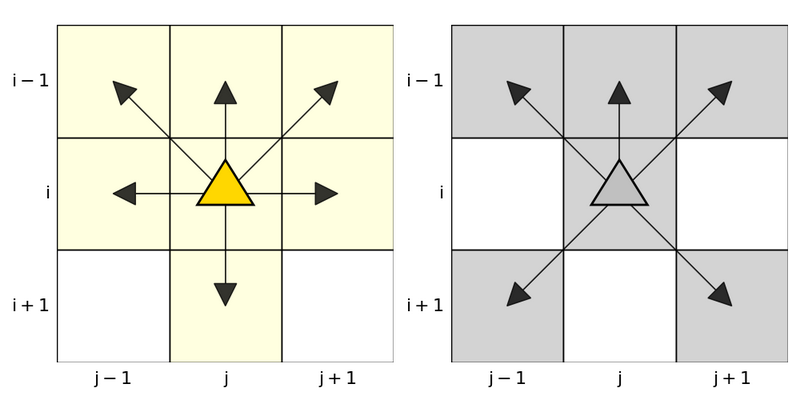
無限に広い二次元グリッドがあります。 グリッド上には $ N $ 人の人がおり、 $ i $ 人目の人ははじめマス $ (R_{i} ,C_{i}) $ にいます。各人は金か銀、いずれかの色の帽子をかぶっています。 $ i $ 人目の人は $ H_i = $ `G` のとき金色、 $ H_i = $ `S` のとき銀色の帽子をかぶっています。 $ 1 $ ターンごとに、各人は帽子の色に応じて、現在地から以下のように移動することができます。 - 金色の帽子をかぶっている人： その場にとどまるか、将棋の金の動きをする。厳密には、現在いるマスを $ (i, j) $ としてマス $ (i-1, j-1), (i-1, j), (i-1, j+1), (i, j-1), (i, j), (i, j+1), (i+1, j) $ のいずれかに移動する。 - 銀色の帽子をかぶっている人： その場にとどまるか、将棋の銀の動きをする。厳密には、現在いるマスを $ (i, j) $ としてマス $ (i-1, j-1), (i-1, j), (i-1, j+1), (i, j), (i+1, j-1), (i+1, j+1) $ のいずれかに移動する。  $ N $ 人全員が同じマスに集まるために必要な最小のターン数を求めてください。 $ T $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

入力は以下の形式で与えられる。 > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ ここで、 $ \mathrm{case}_i $ は $ i $ 番目のテストケースを表す。各テストケースは以下の形式で与えられる。 > $ N $ $ R_1 $ $ C_1 $ $ H_1 $ $ R_2 $ $ C_2 $ $ H_2 $ $ \vdots $ $ R_N $ $ C_N $ $ H_N $

$ T $ 個のテストケースについて答えを改行区切りで出力せよ。

### 部分点 追加の制約 $ H_i = $ `G` を満たすデータセットに正解した場合は $ 30 $ 点が与えられる。 ### Sample Explanation 1 $ 1 $ 個目のテストケースについて、例えば以下のような移動を行うことで、 $ 2 $ ターンで全員同じマスに集まることができます。 - $ 1 $ ターン目 - 人 $ 1 $ は $ (2, 2) $ に移動する - 人 $ 2 $ は $ (3, 3) $ に移動する - $ 2 $ ターン目 - 人 $ 1 $ はその場にとどまる - 人 $ 2 $ は $ (2, 2) $ に移動する $ 2 $ 個目のテストケースについて、例えば以下のような移動を行うことで、 $ 2 $ ターンで全員同じマスに集まることができます。 - $ 1 $ ターン目 - 人 $ 1 $ は $ (1, 2) $ に移動する - 人 $ 2 $ は $ (1, 3) $ に移動する - 人 $ 3 $ は $ (1, 2) $ に移動する - $ 2 $ ターン目 - 人 $ 1 $ はその場にとどまる - 人 $ 2 $ は $ (1, 2) $ に移動する - 人 $ 3 $ はその場にとどまる $ 3 $ 個目のテストケースについて、はじめから全員同じマスに集まっています。 ### Sample Explanation 2 $ 1 $ 個目のテストケースについて、例えば以下のような移動を行うことで、 $ 2 $ ターンで全員同じマスに集まることができます。 - $ 1 $ ターン目 - 人 $ 1 $ は $ (2, 1) $ に移動する - 人 $ 2 $ は $ (2, 2) $ に移動する - $ 2 $ ターン目 - 人 $ 1 $ はその場にとどまる - 人 $ 2 $ は $ (2, 1) $ に移動する この入力例は、部分点の制約を満たします。 ### Constraints - $ T, N, R_i, C_i $ は整数 - $ 1 \le T \le 10^5 $ - $ 1 \le N \le 2 \times 10^5 $ - $ 1 \le R_i \le 10^9 $ - $ 1 \le C_i \le 10^9 $ - $ H_i $ は `G` か `S` のいずれか - $ 1 $ つの入力の中のテストケースすべてにわたる $ N $ の総和は $ 2 \times 10^5 $ 以下