AT_tenka1_2012_8 大爆発

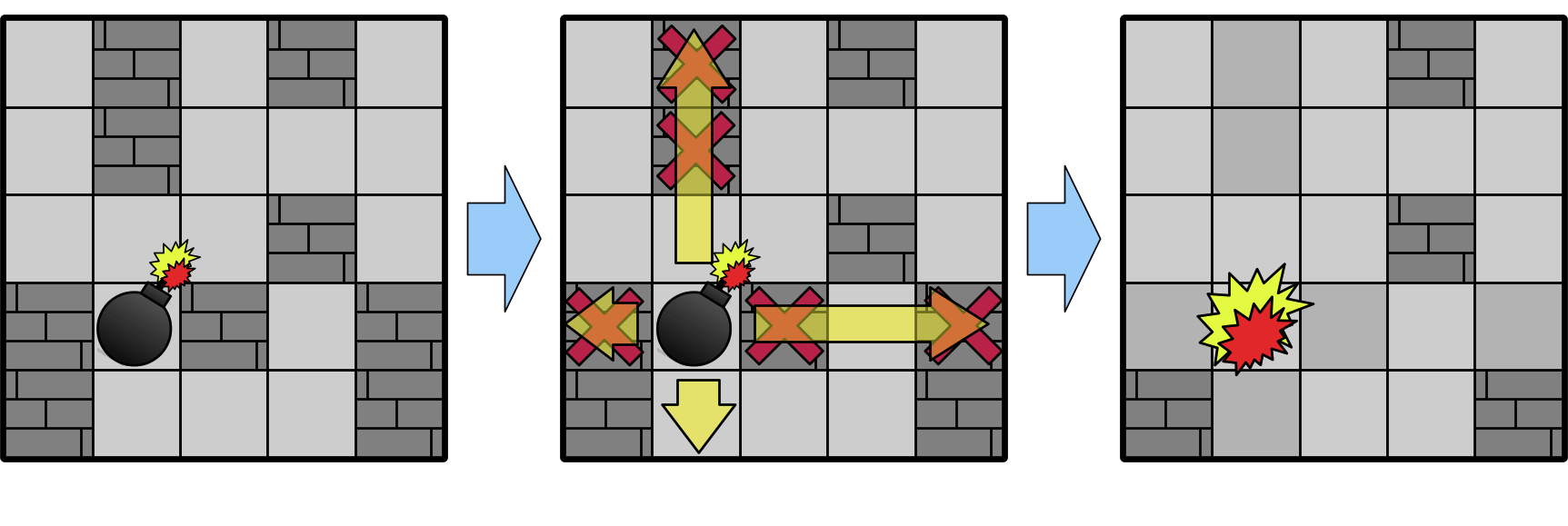
给定一个由格子组成的舞台，你需要用炸弹将舞台上存在的所有方块全部摧毁。 炸弹只能放在没有方块的格子上，放置后会立即爆炸，并摧毁其上下左右所有的方块。 例如，在如图 $1$ 所示的舞台上，如果在坐标 $(1,3)$ 处放置炸弹，则可以摧毁上下左右 $5$ 个方块。 本题中，坐标的定义为舞台左上角的格子为 $(0,0)$，向右一格为 $(1,0)$，向下一格为 $(0,1)$。 即使炸弹与方块之间不相邻（如图 $1$ 中炸弹上方的方块），也可以被摧毁，并且无论连续有多少个方块，都会全部被摧毁。 同样，即使方块之间不相邻（如图 $1$ 中炸弹右侧的方块），也都会被摧毁。  图 $1$ ：炸弹摧毁方块的示例 请你计算，为了摧毁舞台上所有的方块，最少需要放置多少个炸弹。 如果无法摧毁所有方块，则输出 $-1$。 输入以如下格式从标准输入给出： $H$ $W$ $c_{(0,0)}c_{(1,0)}\ldots c_{(W-1,0)}$ $c_{(0,1)}c_{(1,1)}\ldots c_{(W-1,1)}$ $\vdots$ $c_{(0,H-1)}c_{(1,H-1)}\ldots c_{(W-1,H-1)}$ - 输入共 $H+1$ 行。 - 第 $1$ 行为两个整数，分别表示舞台的高 $H$ $(1 \leq H \leq 16)$ 和宽 $W$ $(1 \leq W \leq 16)$，以空格分隔。 - 接下来的 $H$ 行，每行 $W$ 个字符，表示舞台每个格子的状态 $c_{(i,j)}$ $(0 \leq i \leq W-1,\ 0 \leq j \leq H-1)$。 - $c_{(i,j)}$ 取以下两种值之一，分别表示坐标 $(i,j)$ 的格子的状态： - `.` ：该格子没有方块，可以放置炸弹。 - `#` ：该格子有方块，不能放置炸弹。 如果只对小尺寸舞台（$1 \leq W \leq 5,\ 1 \leq H \leq 5$）的输入给出正确答案，则可获得 $100$ 分满分中的 $50$ 分部分分。 请输出使舞台上不再存在任何方块所需的最小炸弹数。如果无法做到，则输出 $-1$。 请注意，输出时行末需换行。 ``` 5 5 .#.#. .#... ...#. #.#.# #...# ``` ``` 2 ``` - 初始状态如图 $1$，首先在坐标 $(1,3)$ 处放置炸弹，可以摧毁坐标 $(0,3),\ (1,0),\ (1,1),\ (2,3),\ (4,3)$ 的方块。 - 然后在坐标 $(3,4)$ 处放置炸弹，可以摧毁剩余的所有方块。 - 因此，最少需要 $2$ 个炸弹。 ``` 5 5 .#... .#... ##### .#... .#... ``` ``` 3 ``` - 首先在坐标 $(0,1)$ 处放置炸弹，可以摧毁 $(0,2)$ 和 $(1,1)$ 的方块。 - 然后在坐标 $(1,1)$ 处放置炸弹，可以摧毁 $(1,0),\ (1,2),\ (1,3),\ (1,4)$ 的方块。 - 最后在坐标 $(1,2)$ 处放置炸弹，可以摧毁剩余的方块。 - 因此，最少需要 $3$ 个炸弹。 ``` 1 6 ###### ``` ``` -1 ``` - 没有任何格子可以放置炸弹，无法摧毁方块。 ``` 3 2 .. .. .. ``` ``` 0 ``` - 初始状态下没有任何方块，无需放置炸弹。

第一行包含两个整数 $H$ 和 $W$，分别表示舞台的高和宽。 接下来的 $H$ 行，每行 $W$ 个字符，表示舞台每个格子的状态。

输出一个整数，表示摧毁所有方块所需的最小炸弹数。如果无法摧毁所有方块，则输出 $-1$。

无。 由 ChatGPT 4.1 翻译