AT_tenka1_2012_final_e GO!GO! サイコロ線路
Description
[problemUrl]: https://atcoder.jp/contests/tenka1-2012-final/tasks/tenka1_2012_final_e
$ N\ ×\ N $ 個のサイコロが $ XY $ 平面上に下図のように配置されています。
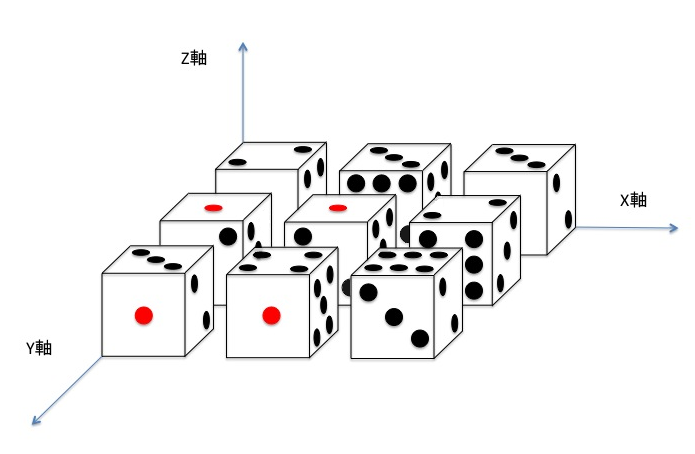
隣接している面の数字が同じサイコロに移動することができ、貴方は左上のサイコロから右下のサイコロへ移動したいです。
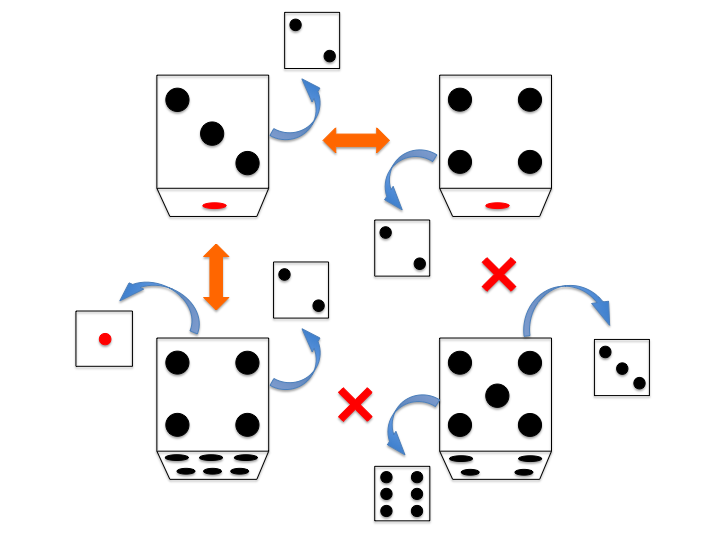
サイコロを $ 90° $ 回転させることができる回数が与えられたとき、経由しなければならないサイコロの最小数を出力しなさい。
また、左上から右下へ移動できないときは `-1` を出力しなさい。
なお、一度移動し始めたら、それ以降サイコロを回転することは出来ません。 入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ c_{00Z} $$ c_{00X} $ $ c_{01Z} $$ c_{01X} $ $ c_{02Z} $$ c_{02X} $ $ … $ $ c_{0(N-1)Z} $$ c_{0(N-1)X} $ $ c_{10Z} $$ c_{10X} $ $ c_{11Z} $$ c_{11X} $ $ c_{12Z} $$ c_{12X} $ $ … $ $ c_{1(N-1)Z} $$ c_{1(N-1)X} $ $ : $ $ : $ $ c_{(N-1)0Z} $$ c_{(N-1)0X} $ $ c_{(N-1)1Z} $$ c_{(N-1)1X} $ $ c_{(N-1)2Z} $$ c_{(N-1)2X} $ $ … $ $ c_{(N-1)(N-1)Z} $$ c_{(N-1)(N-1)X} $
- 入力は $ N+1 $ 行ある。
- $ 1 $ 行目にはサイコロを敷き詰めたときの縦と横の長さ $ N\ (1≦N≦6) $ と、サイコロを回転させることのできる回数 $ M\ (0≦M≦1,000) $ が与えられる。
- $ 2 $ 行目から $ N+1 $ 行目までの $ N $ 行はサイコロの情報を示し、`1` から `6` までの整数 $ 2 $ 桁ごとに半角スペースで区切られている。
- サイコロの情報は $ 2 $ つの整数 $ i\ (0≦i≦N-1) $、$ j\ (0≦j≦N-1) $を用いて以下のように示されている。
1. $ c_{ijZ} $ … $ Z $ 軸正方向に面し、座標 $ (x_i,y_j) $ にあるサイコロの値
2. $ c_{ijX} $ … $ X $ 軸正方向に面し、座標 $ (x_i,y_j) $ にあるサイコロの値
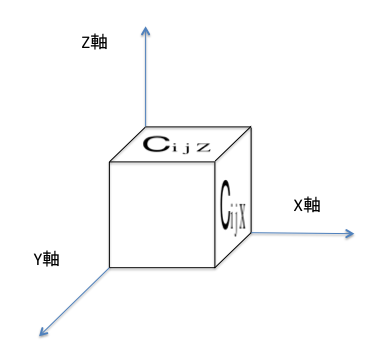
14. $ M $ はサイコロを回転させることができる回数で、サイコロの回転は以下のように定義されている。
1. $ Z $ に対して $ 90° $ 回転することを $ 1 $ 回とカウントする。
2. $ X $ に対して $ 90° $ 回転することを $ 1 $ 回とカウントする。
3. $ Y $ に対して $ 90° $ 回転することを $ 1 $ 回とカウントする。
4. つまり、サイコロの回転軸は $ 3 $ つ存在する。
テストデータには以下に示す $ 4 $ 種類のデータセットのいずれかが含まれており、それぞれサイコロを敷き詰めたときの縦と横の長さを表す $ N $ の範囲が異なっている。
あるデータセットに対して全て正しい解を出力すると、それ以外のデータセットで不正解を出力しても以下のように部分点が与えられる。 - level1 (25 点) : $ N≦3 $
- level2 (25 点) : $ N≦4 $
- level3 (25 点) : $ N≦5 $
- level4 (25 点) : $ N≦6 $
サイコロ $ c_{00} $ からサイコロ $ c_{(N-1)(N-1)} $ へ移動するときに経由しなければならないサイコロの最小値。
サイコロ $ c_{00} $ からサイコロ $ c_{(N-1)(N-1)} $ へ到達不能な場合は、`-1` を出力せよ。
なお、出力の終端には改行が必要である。
この問題で使用するサイコロの展開図と、それを組み立てたものを以下に示す。
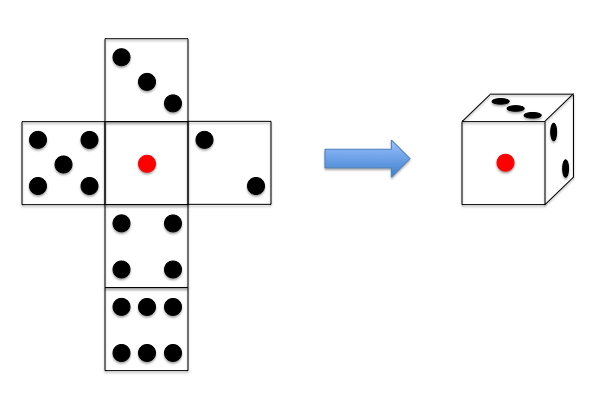
Input Format
N/A
Output Format
N/A