AT_tenka1_2012_final_e GO!GO! サイコロ線路
题目描述
在 $XY$ 平面上,$N \times N$ 个骰子按照下图方式排列。
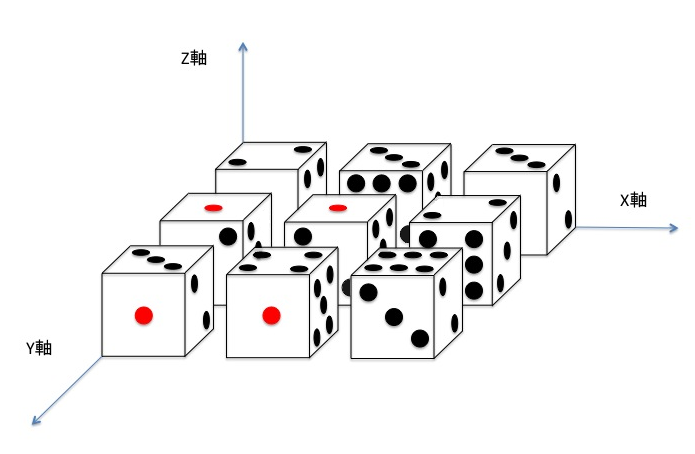
你可以在相邻的骰子之间移动,前提是相邻面上的数字相同。你希望从左上角的骰子移动到右下角的骰子。
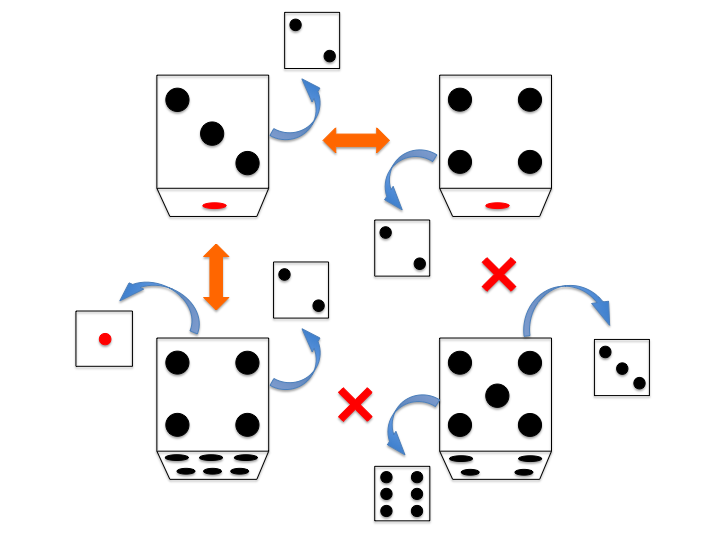
给定你可以将骰子旋转 $90^\circ$ 的次数,输出从起点到终点必须经过的最小骰子数。
如果无法从左上角移动到右下角,则输出 $-1$。
注意,一旦开始移动,就不能再旋转骰子。输入格式如下:
> $N$ $M$ $c_{00Z}$ $c_{00X}$ $c_{01Z}$ $c_{01X}$ $c_{02Z}$ $c_{02X}$ $\dots$ $c_{0(N-1)Z}$ $c_{0(N-1)X}$ $c_{10Z}$ $c_{10X}$ $c_{11Z}$ $c_{11X}$ $c_{12Z}$ $c_{12X}$ $\dots$ $c_{1(N-1)Z}$ $c_{1(N-1)X}$ $:$ $:$ $c_{(N-1)0Z}$ $c_{(N-1)0X}$ $c_{(N-1)1Z}$ $c_{(N-1)1X}$ $c_{(N-1)2Z}$ $c_{(N-1)2X}$ $\dots$ $c_{(N-1)(N-1)Z}$ $c_{(N-1)(N-1)X}$
- 输入共 $N+1$ 行。
- 第 $1$ 行给出骰子排列的行列数 $N\ (1 \leq N \leq 6)$ 和可以旋转骰子的次数 $M\ (0 \leq M \leq 1000)$。
- 第 $2$ 行到第 $N+1$ 行的 $N$ 行给出骰子的信息,每行用空格分隔的两个整数,取值为 $1$ 到 $6$。
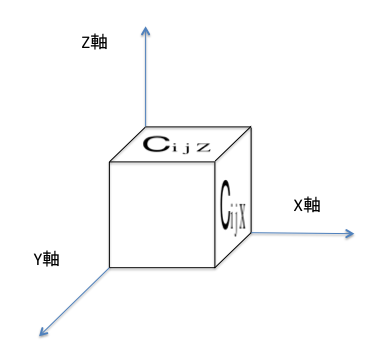
- 骰子的信息用 $i\ (0 \leq i \leq N-1)$、$j\ (0 \leq j \leq N-1)$ 表示,具体如下:
1. $c_{ijZ}$:在坐标 $(x_i, y_j)$ 处,朝 $Z$ 轴正方向的骰子面上的数字。
2. $c_{ijX}$:在坐标 $(x_i, y_j)$ 处,朝 $X$ 轴正方向的骰子面上的数字。
- $M$ 表示可以旋转骰子的次数,骰子的旋转定义如下:
1. 围绕 $Z$ 轴旋转 $90^\circ$ 记为 $1$ 次。
2. 围绕 $X$ 轴旋转 $90^\circ$ 记为 $1$ 次。
3. 围绕 $Y$ 轴旋转 $90^\circ$ 记为 $1$ 次。
4. 即骰子的旋转轴有 $3$ 种。
测试数据包含如下 $4$ 种数据集,每种数据集的 $N$ 范围不同。对于某一数据集全部输出正确,即使其他数据集输出错误,也可获得部分分数。
- level1(25分):$N \leq 3$
- level2(25分):$N \leq 4$
- level3(25分):$N \leq 5$
- level4(25分):$N \leq 6$
请输出从骰子 $c_{00}$ 到骰子 $c_{(N-1)(N-1)}$ 所需经过的最小骰子数。
如果无法从 $c_{00}$ 到达 $c_{(N-1)(N-1)}$,则输出 $-1$。
输出末尾需换行。
本题所用骰子的展开图及其组装后的样子如下所示。
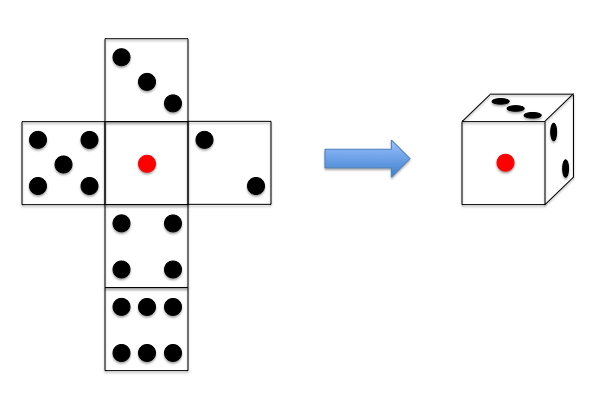
输入格式
第 $1$ 行包含两个整数 $N$ 和 $M$,分别表示骰子的行列数和可以旋转的次数。
接下来 $N$ 行,每行包含 $2N$ 个整数,依次为每个骰子在该行的 $Z$ 轴正方向和 $X$ 轴正方向的数字。
输出格式
输出一个整数,表示从左上角到右下角所需经过的最小骰子数。如果无法到达,则输出 $-1$。输出末尾需换行。
说明/提示
由 ChatGPT 4.1 翻译