AT_tenka1_2012_qualA_4 アリの巣

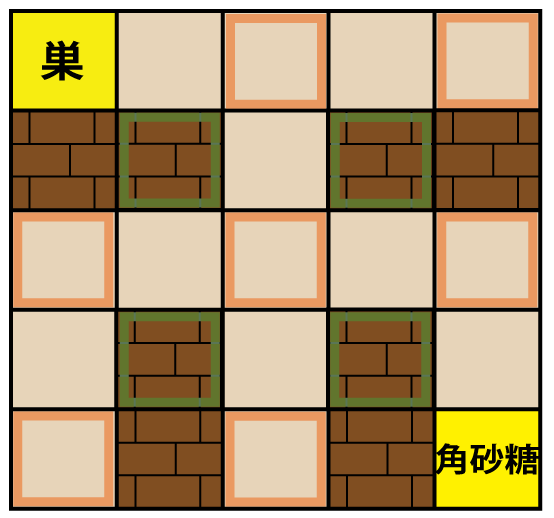
有一个由方格组成的迷宫。 迷宫中的每个方格可能是巢、糖块、墙壁或空地。蚂蚁们希望从左上角巢所在的方格出发，到达右下角糖块所在的方格。 蚂蚁可以到达任何不是墙壁的方格，包括糖块所在的方格，且路径中不形成环。 特别地，坐标为（奇数, 奇数）的方格一定是墙，而（偶数, 偶数）的方格一定是空地。 坐标系统以左上角的巢位置为起点 $(0,0)$，向右一个单位为 $(1,0)$，向下一个单位为 $(0,1)$。 图 $1$ 展示了这样的迷宫示例。 黄绿色的部分表示（奇数, 奇数）的墙壁位置，橙色的部分表示（偶数, 偶数）的空地位置。  图 $1$：迷宫示例 蚂蚁具有以下特性：当可以直行时，它总是选择直行；如果它撞到墙，会有 $1/2$ 的概率向左转，$1/2$ 的概率向右转。如果其撞墙并且左右两边之一也是墙，那么它必定会转向另一侧的开放区域。 若遇到三面都是墙或迷宫的边界而无法转弯，蚂蚁会原地死亡并变成墙。 需要注意的是，巢下方的方格是墙，因此蚂蚁一开始只能向右走。糖块左侧的方格也是墙，所以蚂蚁只能从上方到达糖块位置。 例如，在图 $1$ 的示例中，如图 $2$ 所示，第一只蚂蚁会直行，最后在右上方的 $(4,0)$ 被墙与迷宫边界包围而死亡。 第二只蚂蚁在 $(3,0)$ 死亡，因为 $(4,0)$ 已被第一只蚂蚁占据并变为墙。 于是，第三只和第四只蚂蚁在 $(2,0)$ 处向右转，分别在 $(2,4)$ 和 $(2,3)$ 处死亡。 第五只蚂蚁到达 $(2,2)$ 时无法直行，需要向 $(1,2)$ 或 $(3,2)$ 转向。 若向 $(1,2)$ 移动，它将在 $(0,4)$ 处死亡；若向 $(3,2)$ 移动，则可成功到达糖块。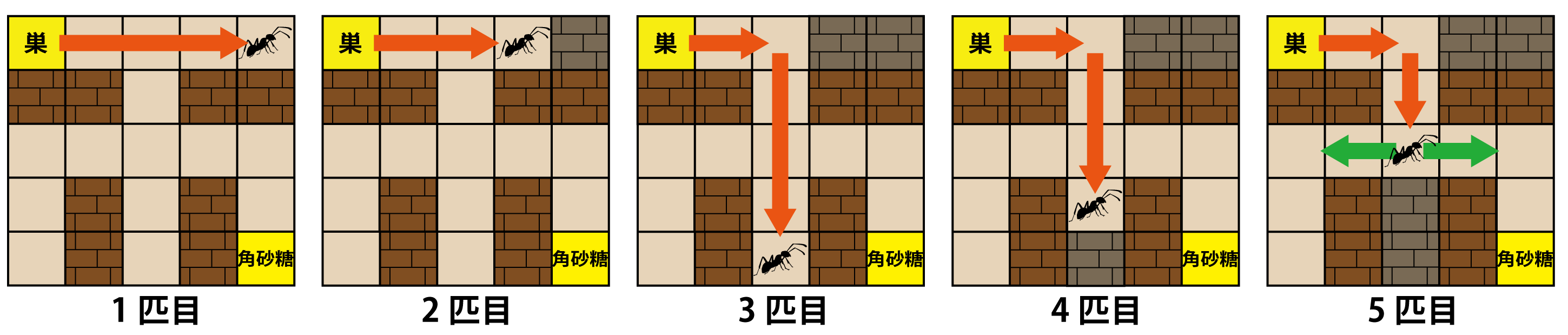  图 $2$：图 $1$ 中迷宫对前五只蚂蚁的行动记录 请计算蚂蚁达到糖块所需数量的期望值。 **本翻译由 AI 自动生成**

- 第一行输入一个整数 $N(5 \le N \le 49)$，代表迷宫的宽和高。 - **注意：** $N$ 为奇数。 - 接下来的 $N$ 行，每行包含 $N$ 个字符，表示迷宫的状态 $c_{(i,j)}(0 \le i, j \le N-1)$。 - 其中，$c_{(i,j)}$ 可以是以下字符之一： - `S`：表示该位置为巢。 - `G`：表示该位置有糖块。 - `#`：表示该位置为墙。 - `.`：表示该位置为空地。 - $c_{(0,0)}$ 必为 `S`，且 $c_{(N-1,N-1)}$ 必为 `G`，并各自在唯一的位置。 - 巢下方的一个位置 $c_{(1,0)}$ 和糖块左方的一个位置 $c_{(N-1,N-2)}$ 必为 `#`。 - 两者坐标均为奇数的地点必为 `#`，而均为偶数的则必为 `.`。

输出一个浮点数，表示蚂蚁到达糖块所在方格所需的期望数量，结果保留到小数点后六位。 误差要求：绝对误差或相对误差至少有一种不超过 $10^{-6}$。 需要在结果数字的行末添加换行符。