AT_tenka1_2013_final_a 天下一有無

天下一株式会社正在制造一种顶级的物质 Tenkaitium。Tenkaitium 是制造下一代量子计算机不可或缺的物质。 优也君被分配到了 Tenkaitium 的运营与管理团队。入职后，优也君的第一项工作是为了搬运而将 Tenkaitium 放入容器中。然而，Tenkaitium 有一个特性：当超过一定数量的该物质彼此靠近时，它就会转变成 Tenka$\text{\color{red}{ni}}$tium（遗憾的是，Tenka$\text{\color{red}{ni}}$tium 没有任何产业价值）。 因此，优也君将容器划分为 $N \times M$ 的网格。每个格子中至多放一个 Tenkaitium，且不存在两个含 Tenkaitium 的格子有至少一个公共点（即不能横向、纵向或者斜向相邻）。 求至少放置一个 Tenkaitium 的合法方案数对 $10^9+7$ 取模的结果。两种方案被视为不同的，当且仅当存在至少一个格子，它在某一种方案中含有 Tenkaitium，但在另一种方案中不含有 Tenkaitium。

一行两个正整数 $N$ 和 $M$，表示容器的长与宽。

一行一个整数，表示合法方案数对 $10^9+7$ 取模的结果。 注意，**在行尾需要换行**！

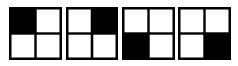
$1 \le N ,M \le 15$。 #### 【样例解释 1】  #### 【样例解释 2】