AT_tenka1_2013_qualB_e 天下一最短路コンテスト

你是天下一最短路竞赛的主办者。 天下一最短路竞赛按照如下规则举办： - 在二维平面上给定 $N$ $(1 \leq N \leq 100)$ 个点 $p_i$ $(1 \leq i \leq N)$。 - 点 $p_i$ 的 $x$ 坐标为 $x_i$，$y$ 坐标为 $y_i$。 - 点的数量 $N$ 最大为 $100$。 - 各坐标的值 $x_i$、$y_i$ 均为不超过 $10,000$ 的非负整数。 - 所有点的坐标均不相同。即当 $i \neq j$ 时，$(x_i, y_i) \neq (x_j, y_j)$。 - 从 $p_1$ 出发，输出一条经过所有点的路径。 - 路径长度最短的人获胜。 高桥君打算参加天下一最短路竞赛，但他觉得自己赢不了对手——KLab 的超级程序员タクヤ君。タクヤ君的程序是开源的，高桥君打算通过改造它来争取胜利。 タクヤ君的程序如下： - 首先选择点 $p_1$，只要还有未被选择的点，按以下步骤选择下一个点： - 从最后选择的点出发，选择距离最近的、尚未被选择的点。 - 如果有多个距离最近的点，则选择编号最小的那个（点 $p_i$ 的编号为 $i$）。 - 按照被选择的顺序，用线段连接这些点，输出这条路径。 高桥君改造后的程序如下： - 首先选择点 $p_1$，只要还有未被选择的点，按以下步骤选择下一个点： - 如果未被选择的点数不少于 $3$，则从最后选择的点出发，选择距离第二近的点。 - 此时，即使最近的点在最后选择的点与第二近的点连线的直线上，也不认为最近的点被选择。 - 如果未被选择的点数不超过 $2$，则从最后选择的点出发，选择最近的点。 - 注意，最近的点会被选择两次，而不是只在最后一次被选择。 - 如果有多个距离相同的点，则编号小的点视为更近。 - 按照被选择的顺序，用线段连接这些点，输出这条路径。 让这两个程序对战后，几乎每次高桥君都输了。但这样高桥君太可怜了，所以你需要为高桥君准备一个至少能打平的输入数据集，并且点数尽可能多。 输入无需给出。请输出一个使高桥君至少能打平的数据集，输出格式如下： > $N$ > $x_1$ $y_1$ > $x_2$ $y_2$ > ... > $x_N$ $y_N$ 1. 第 $1$ 行输出数据集的点数 $N$ $(1 \leq N \leq 100)$。 2. 第 $2$ 行起，每行输出一个点的 $x$ 坐标 $x_i$ 和 $y$ 坐标 $y_i$，用空格分隔，共 $N$ 行，$0 \leq x_i, y_i \leq 10,000$。 3. 只要数据集满足条件，就能获得 $N \times 2$ 分。 如果两个程序输出的路径长度的绝对差或相对差不超过 $10^{-9}$，则视为平局。 即，若两程序输出的路径长度分别为 $d_1$、$d_2$，则若 $\frac{|d_1 - d_2|}{\max(1, d_1, d_2)} \leq 10^{-9}$，则视为平局。 输出末尾需换行。 你也可以直接提交事先计算好的输出结果，此时请选择 Text(cat) 作为提交语言。 ``` 1 1 1 ``` - 当点数为 $1$ 时，两程序输出的路径长度均为 $0$，为平局。 - 提交该输出可获得 $2$ 分。 ``` 5 4 6 2 5 6 10 1 2 1 6 ``` - タクヤ君的程序得到的路径为 $(4,6) \to (2,5) \to (1,6) \to (1,2) \to (6,10)$，路径长度约为 $17.084$。 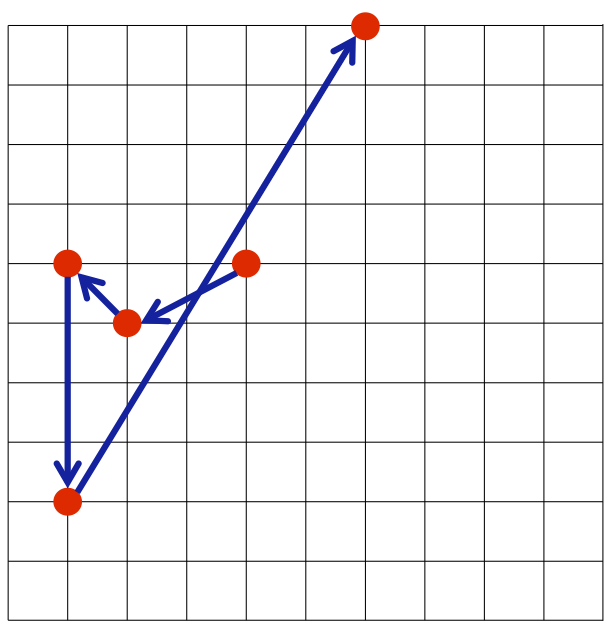 图 $1$ タクヤ君的程序路径 - 高桥君的程序得到的路径为 $(4,6) \to (1,6) \to (1,2) \to (2,5) \to (6,10)$，路径长度约为 $16.565$。 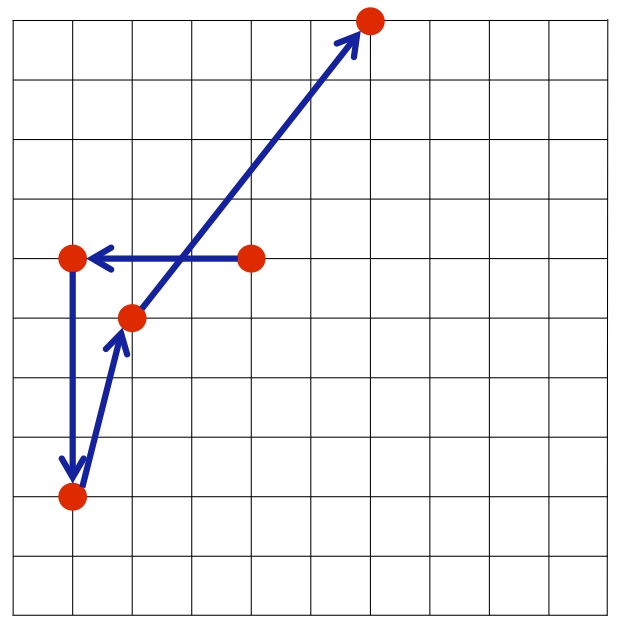 图 $2$ 高桥君的程序路径 - 提交该输出可获得 $10$ 分。

无输入。

第 $1$ 行输出点的数量 $N$。 第 $2$ 行起，每行输出一个点的 $x$ 坐标 $x_i$ 和 $y$ 坐标 $y_i$，用空格分隔，共 $N$ 行。 输出末尾需换行。

无。 由 ChatGPT 4.1 翻译