AT_tenka1_2013_qualB_e 天下一最短路コンテスト

[problemUrl]: https://atcoder.jp/contests/tenka1-2013-qualb/tasks/tenka1_2013_qualB_e あなたは、天下一最短路コンテストの運営者です。 天下一最短路コンテストでは、以下のようなルールで開催されます。 - 二次元平面上に $ N $ $ (\ 1\ ≦\ N\ ≦\ 100) $ 個の点 $ p_i $ $ (\ 1\ ≦\ i\ ≦\ N\ ) $ が与えられます - 点 $ p_i $ の$ x $ 座標は $ x_i $ で $ y $ 座標は $ y_i $ です - 点の数 $ N $ は最大 $ 100 $ 個です - 各座標の値 $ x_i $, $ y_i $ は全て $ 10,000 $ 以下の非負の整数です - 全ての点の座標は異なります。つまり、$ i\ ≠\ j $ のとき、$ (x_i,\ y_i)\ ≠\ (x_j,\ y_j) $ を満たします - $ p_1 $ から始まり、全ての点を通る経路を出力します - 経路の長さが最も短い人の勝ちです 高橋君は、天下一最短路コンテストに出場しようとしていますが、ライバルである、KLabのスーパープログラマー、タクヤ君に勝てる気がしません。タクヤ君のプログラムは、オープンソースとして公開されていたので、これを改造することで、コンテストに勝とうと考えました。 タクヤ君のプログラムは、以下のようなプログラムです。 - 最初に点 $ p_1 $ を選び、まだ選んでいない点が存在する間、以下の手順で点を選ぶ - 最後に選んだ点から、最も近い、まだ選んでいない点を選ぶ - 最も近い点が複数ある場合は、その中でidが一番小さいものを選ぶ（点 $ p_i $ のidは $ i $ ） - 点を選ばれた順番に、線分で結んで、それを経路として出力する このプログラムを、高橋君が改造した結果、以下のようになりました。 - 最初に点 $ p_1 $ を選び、まだ選んでいない点が存在する間、以下の手順で点を選ぶ - まだ選んでいない点が $ 3 $ つ以上ある場合、最後に選んだ点から $ 2 $ 番目に近い点を選ぶ - この際、最も近い点が、最後に選んだ点と $ 2 $ 番目に近い点とを結ぶ線分の上にあったとしても、最も近い点は選ばれたとみなされない - まだ選んでいない点が $ 2 $ つ以下の場合、最後に選んだ点から最も近い点を選ぶ - 最も近い点が選ばれるのは、最後の $ 1 $ 回ではなく、 $ 2 $ 回であることに注意してください - 同じ距離の点が複数ある場合は、idの小さいものほど近い点であるとみなす - 点を選ばれた順番に、線分で結んで、それを経路として出力する この $ 2 $ つのプログラムを戦わせてみたところ、殆どの場合で、高橋君が負けてしまいます。ですが、このままだと高橋君が可哀想なので、高橋君が引き分け以上の結果を残せる入力を１つだけ用意することにしました。 あなたは、高橋君が引き分け以上の結果を出す、可能な限り頂点数の多いデータセットを作らなければいけません。 入力は与えられない。 高橋君が引き分け以上の結果を出すことができるデータセットを出力しなさい。出力は以下の形式で行う。 > $ N $ $ x_1 $ $ y_1 $ $ x_2 $ $ y_2 $ : $ x_N $ $ y_N $ 1. $ 1 $行目には、データセットの頂点数 $ N\ (1≦N≦100) $ を $ 1 $ 行で出力する 2. $ 2 $行目には、各点の $ x $ 座標 $ x_i $、$ y $ 座標 $ y_i $を、$ x_i $ $ y_i $の順でスペース区切りに、$ N $行で出力する $ (\ 0\ ≦\ x_i,\ y_i\ ≦\ 10,000) $ 3. 条件を満たすデータセットであれば、$ N×2 $点の点数が得られます。 二つのプログラムの出力する経路の長さの、絶対的な差または相対的な差が $ 10^{-9} $以下であれば、二つのプログラムは引き分けとみなす。 つまり、二つのプログラムの出力する経路の長さがそれぞれ$ d_1 $, $ d_2 $であるとき、$ \frac{|d_1\ -\ d_2|}{{\rm\ max}(1,\ d_1,\ d_2)}\ ≦\ 10^{-9} $であれば、引き分けとみなす。 また、出力の最後には改行をいれること。 なお、あらかじめ計算して出力した結果を、そのまま提出しても良い。その場合は、使用言語にText(cat)を選択して提出すること。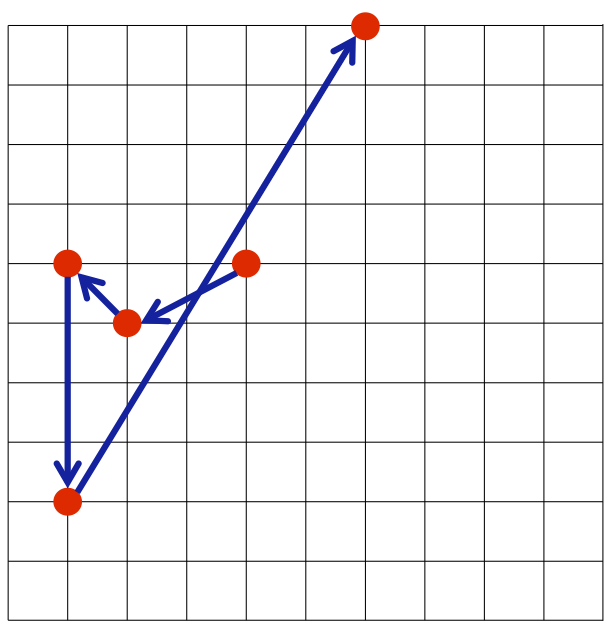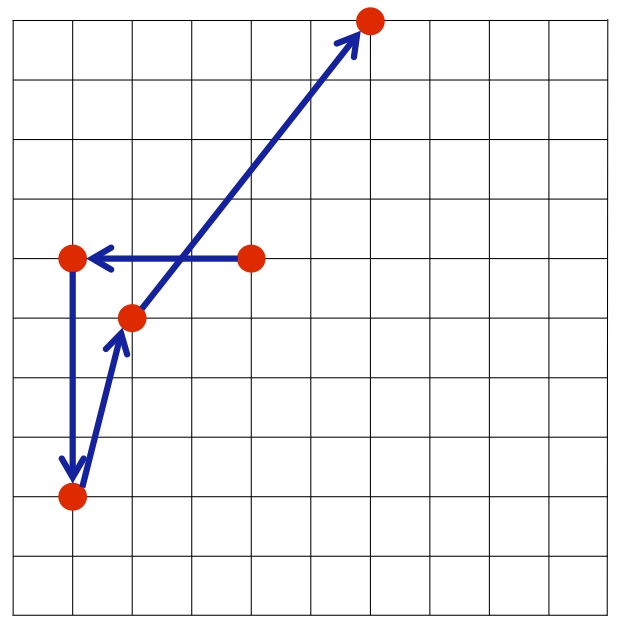 ``` 1 1 1 ``` - 点が $ 1 $ 個の時、どちらのプログラムも出力する経路の長さは $ 0 $ となり、引き分けとなります - この出力を提出すると、 $ 2 $ 点を得ることが出来ます ``` 5 4 6 2 5 6 10 1 2 1 6 ``` - タクヤ君のプログラムが求める経路は、 $ (4,6)\ →\ (2,5)\ →\ (1,6)\ →\ (1,2)\ →\ (6,10) $であり、この経路の長さは約$ 17.084 $です 図 $ 1 $タクヤ君のプログラムの経路 - 高橋君のプログラムが求める経路は、 $ (4,6)\ →\ (1,6)\ →\ (1,2)\ →\ (2,5)\ →\ (6,10) $であり、この経路の長さは約$ 16.565 $です 図 $ 2 $高橋君のプログラムの経路 - この出力を提出すると、 $ 10 $ 点を得ることができます

N/A

N/A