AT_tenka1_2014_qualA_d EMLauncher

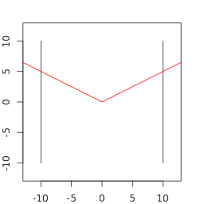
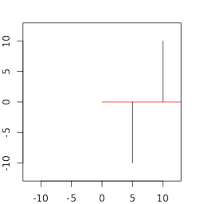
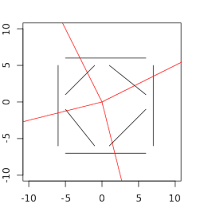
在天下一王国，测试一种新开发的高科技武器——电磁炮（ElectroMagneticLauncher）。测试的目标是击穿所有摆放在场地上的 $N$ 块铁板。理论上，电磁炮的威力足以穿透任意多的障碍物，但每次发射都会消耗大量的电力。因此，如何计算出最少的发射次数来破坏所有障碍物成了大辉君的任务。炮座可以调整方向朝任意方向发射。 为了便于分析，障碍物可以看作平面坐标系中的线段，电磁炮则位于原点 $(0, 0)$。每次发射形成的弹体轨迹可以看作从原点射出的半直线，能摧毁所有与之相交或接触的障碍物。  图中射击红线方向，两次可完成任务。  因为两块障碍物接触到红线，一次射击即完成任务。  图中射击红线方向，需四次射击完成任务。

输入包括以下信息： - 第一行是一个整数 $N$，表示障碍物的数量，满足 $1 \leq N \leq 2000$。 - 接下来的 $N$ 行，每行有四个整数，分别是每个障碍物的两个端点坐标：$(X_{i,1}, Y_{i,1})$ 和 $(X_{i,2}, Y_{i,2})$，它们满足 $-1000 \leq X_{i,1}, Y_{i,1}, X_{i,2}, Y_{i,2} \leq 1000$。 - 这些障碍物（包括端点）不会碰到原点，也不会相互交叉或接触。

输出一个整数，表示击穿所有障碍物所需的最小发射次数。输出需要换行。

- 当 $N \leq 20$ 时，通过所有测试可得 $45$ 分。 - 当 $N \leq 200$ 时，通过所有测试可再得 $40$ 分。 **本翻译由 AI 自动生成**