AT_tenka1_2015_final_e 天下一コップ

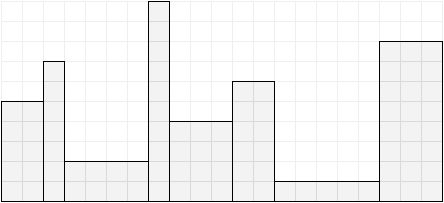[problemUrl]: https://atcoder.jp/contests/tenka1-2015-final/tasks/tenka1_2015_final_e $ N $ 個の長方形がある。 $ i $ 番目の長方形は幅が $ w_i $ で高さが $ h_i $ である。 $ N $ 個の長方形を好きな順序で並べてコップを作る。 このとき、それぞれの長方形は回転させずに、すべての長方形の底辺が一直線上にあるようにする。 また、隣り合う長方形同士がちょうど接するようにする。 図 1 : コップの例 コップを水で満杯にすることを考える。 このとき、座標 $ P $ に水が存在するための必要十分条件は以下である。 - $ P $ はどの長方形の内部にもない。 - $ P $ から左および右向きへ半直線を引いたとき、どちらの半直線もいずれかの長方形と共有点を持つ。 コップを水で満杯にしたとき、水が存在する領域の総面積を *容積* と呼ぶ。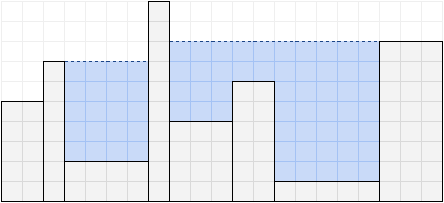 図 2 : コップを水で満杯にした例 (容積 71) 長方形を並べてコップを作る作り方は全部で $ N! $ 通りである。それら $ N! $ 通りのコップの容積の和を $ 10^9+7 $ で割った余りを求めよ。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ w_1 $ $ h_1 $ $ w_2 $ $ h_2 $ $ : $ $ w_N $ $ h_N $ - $ 1 $ 行目には、長方形の個数を表す整数 $ N $ ($ 3≦N≦10^5 $) が与えられる。 - $ 2 $ 行目からの $ N $ 行のうち $ i $ 行目には、$ i $ 番目の長方形の幅と高さを表す整数 $ w_i,h_i $ ($ 1≦w_i,h_i≦10^9 $) が空白区切りで与えられる。

$ N! $ 通りのコップの容積の和を $ 10^9+7 $ で割った余りを出力せよ。 出力の末尾には改行を入れること。

### 部分点 この問題には部分点が設定されている。 - $ 3≦N≦8 $ を満たすデータセットに正解した場合は $ 15 $ 点が得られる。 - $ 3≦N≦2,000 $ を満たすデータセットに正解した場合はさらに $ 55 $ 点が得られる。 - $ 3≦N≦10^5 $ を満たすデータセットに正解した場合はさらに $ 70 $ 点が得られる。合計で $ 140 $ 点となる。 ### Sample Explanation 1 $ 6 $ 通りのコップの容積の和は $ 24 $ である。 !\[\](http://tenka1-2015-final.contest.atcoder.jp/img/other/tenka\_2015\_final/hoge/cup\_3.png) ### Sample Explanation 2 幅および高さが等しい長方形同士も区別して並べる。