AT_tenka1_2015_final_e 天下一コップ

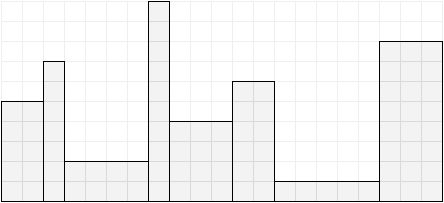
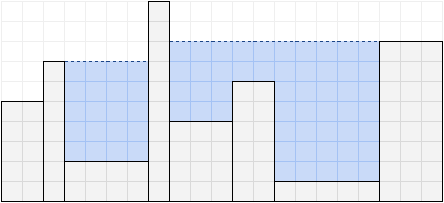
有 $N$ 个长方形。第 $i$ 个长方形的宽为 $w_i$，高为 $h_i$。 你可以以任意顺序排列这 $N$ 个长方形，制作一个“杯子”。在排列时，所有长方形都不能旋转，且所有长方形的底边必须在同一条直线上，相邻的长方形必须恰好相接。  图 1：杯子的例子 现在考虑将杯子装满水。此时，某个坐标 $P$ 存在水的充要条件如下： - $P$ 不在任何一个长方形的内部。 - 从 $P$ 向左和向右分别引出一条射线，这两条射线都必须与某个长方形有公共点。 将杯子装满水后，水所在区域的总面积称为“容积”。  图 2：杯子装满水的例子（容积为 $71$） 排列长方形制作杯子的方式共有 $N!$ 种。请计算这 $N!$ 种杯子的容积之和对 $10^9+7$ 取模的结果。

输入通过标准输入给出。 > $N$ > $w_1\ h_1$ > $w_2\ h_2$ > $\vdots$ > $w_N\ h_N$ - 第 $1$ 行为一个整数 $N$，表示长方形的数量，$3 \leq N \leq 10^5$。 - 接下来的 $N$ 行中，第 $i$ 行包含两个用空格分隔的整数 $w_i, h_i$，分别表示第 $i$ 个长方形的宽和高，$1 \leq w_i, h_i \leq 10^9$。

输出 $N!$ 种杯子的容积之和对 $10^9+7$ 取模的结果。输出末尾需换行。

## 部分分 本题设有部分分。 - 对于满足 $3 \leq N \leq 8$ 的数据集，答对可得 $15$ 分。 - 对于满足 $3 \leq N \leq 2,000$ 的数据集，答对可再得 $55$ 分。 - 对于满足 $3 \leq N \leq 10^5$ 的数据集，答对可再得 $70$ 分。总分为 $140$ 分。 ## 样例解释 1 $6$ 种杯子的容积之和为 $24$。  ## 样例解释 2 宽度和高度相同的长方形也要区分排列。 由 ChatGPT 4.1 翻译