AT_tenka1_2015_qualA_a 展開図プログラマーコンテスト

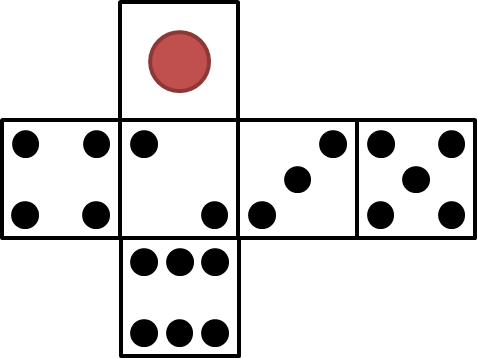
* 安德鲁很喜欢展开图。 * 今天的安德鲁正在考虑 $6$ 面骰子的展开图 * $6$ 面骰子的展开图有几种模式。例如，可以考虑以下内容。  以上是安德鲁是 $6$ 面骰子的展开 首先选择展开图上的任意数字的体量。之后，从那个数字的格子移动到上下左右 $4$ 方向的邻接的格子，为了不通过一次通过的格子而移动，排列通过的格子的数字来制作数量。 * 根据上述的展开图，可以制作 $1235$ 和$326$ 这样的数量。 * 另外，从其他的展开图中，可以制作 $1462$ 和 $354$ 这样的数量。 * 但是，不管是什么样的展开图，都不能制作 $121$ 和 $123456$ 这样的数量。 * 任意选择 $6$ 面骰子的展开图，用这个方法做数的时候，能做的最大的数到底是什么呢? * $1～6$ 的面各具有 $1$ 个。 * 面对面的数量之和为 $7$ 。 * 骰子的雌雄都可以。也就是说，在将 $1$ 个面以天、$6$ 的面为地的方式放置时，$2$ 个面右边的面可以是 $3$ 也可以是 $4。$

在这个问题上不能给出输入。

把能做的最大的数输出到1行，在输出的末尾加上换行。

这个问题没有设置部分点。如果答对了，就给10分